Relatedness of the incidence decay with exponential adjustment (IDEA) model, "Farr's law" and SIR compartmental difference equation models

Abstract

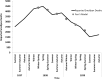
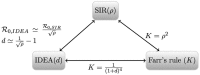
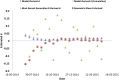
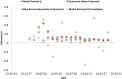
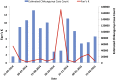
Mathematical models are often regarded as recent innovations in the description and analysis of infectious disease outbreaks and epidemics, but simple mathematical expressions have been in use for projection of epidemic trajectories for more than a century. We recently introduced a single equation model (the incidence decay with exponential adjustment, or IDEA model) that can be used for short-term epidemiological forecasting. In the mid-19th century, Dr. William Farr made the observation that epidemic events rise and fall in a roughly symmetrical pattern that can be approximated by a bell-shaped curve. He noticed that this time-evolution behavior could be captured by a single mathematical formula ("Farr's law") that could be used for epidemic forecasting. We show here that the IDEA model follows Farr's law, and show that for intuitive assumptions, Farr's Law can be derived from the IDEA model. Moreover, we show that both mathematical approaches, Farr's Law and the IDEA model, resemble solutions of a susceptible-infectious-removed (SIR) compartmental differential-equation model in an asymptotic limit, where the changes of disease transmission respond to control measures, and not only to the depletion of susceptible individuals. This suggests that the concept of the reproduction number $\left(R_0\right)$ was implicitly captured in Farr's (pre-microbial era) work, and also suggests that control of epidemics, whether via behavior change or intervention, is as integral to the natural history of epidemics as is the dynamics of disease transmission.

Fig. 1

A recreation of William Farr's possible approach modeling the decline in smallpox mortality in England, 1837–1839 (Farr, 1840). Black line, smallpox mortality by season; gray dots represent Farr's “model projections” derived by assuming a constant additive increase (approximately 5% per season) in the decline in smallpox deaths. Farr “smoothed” reported seasonal deaths by averaging adjacent seasons; hence model projections are plotted at the midpoint (e.g., “winter-spring”, “spring-summer”) at each interval.

Fig. 2

Relationship between the three models. Parameter ρ represent the relative risk of infection in each generation for the SIR model. The control parameter d is associated with the IDEA model and K is Farr's ratio.

Fig. 3

A heat map plotting values for ${\mathcal{R}}_{0,SIR}$ and ρ where the damped SIR model can be approximated by a IDEA model using equations (11), (12). Darker areas indicate a good match (measured as the sum of squared differences) between the simulated incidence time series; lighter areas represent combinations of values for which incidence time series for SIR and IDEA diverge.

Fig. 4

Evaluation of IDEA model fit to simulated data derived from the damped SIR model. Left panel illustrates a scenario where approximation is very good, (${\mathcal{R}}_{0,SIR}=3.5$, $\rho =0.85$), corresponding to a combination of values found in the dark area in Fig. 3. The right sided panel uses a combination of values (high ${\mathcal{R}}_{0,SIR}$ and/or low ρ) where susceptible depletion cannot be ignored (i.e., corresponding to the white area in Fig. 3 3). It can be seen that IDEA and the damped SIR models diverge when susceptibles are rapidly depleted.

Fig. 5

The graph plots estimates of IDEA d parameter against time during the recent West African Ebola outbreak. Approximate date of the last generation incorporated into estimates is plotted on the X-axis; estimated d is plotted on the Y-axis. d estimates were either derived via IDEA model fitting to “incident” cases (blue diamonds) or cumulative incidence (crosses), or derived by estimating Farr's K and transforming resultant estimates using the relation described by equation (9). When K is estimated using 4-generation series (green diamonds), resultant d estimates are volatile and bear little resemblance to d estimates derived through fitting IDEA. However, estimates of K derived as geometric means of all available K values (red squares) provide a more reasonable approximation of d.

Fig. 6

As with Fig. 5, this figure shows estimates of d, derived directly by model fitting or by transforming estimates of Farr's K, for the emerging Western Hemisphere Chikungunya epidemic in 2014–2015. As in Fig. 5, d estimates were either derived via IDEA model fitting to “incident” cases (blue diamonds) or cumulative incidence (crosses), or derived by estimating Farr's K and transforming resultant estimates. As in Fig. 5, volatile estimates of K were derived using 4-generation series (green diamonds), but estimates of K derived as geometric means of all available K values (red squares) provided a reasonable approximation of d.

Fig. 7

A possible application for raw estimates of Farr's K emerged in analysis of data from the 2014–2015 Western Hemisphere Chikungunya outbreak; here it appears that a multi-wave epidemic is signaled by a sudden surge in K to a value $>1$ (red line), indicating that there is renewed exponential growth in cases (blue bars), rather than exponential decline. X-axis, date of most recent generation; left Y-axis, Farr's K; right Y-axis, estimated per-generation Chikungunya case count and transforming resultant estimates. As in Fig. 1, volatile estimates of K were derived using 4-generation series (green diamonds), but estimates of K derived as geometric means of all available K values (red squares) provided a reasonable approximation of d.