COMPOSITIONAL DIVERSITY IN THE ATMOSPHERES OF HOT NEPTUNES, WITH APPLICATION TO GJ 436b
- PMID: 30842681
- PMCID: PMC6398956
- DOI: 10.1088/0004-637X/777/1/34
COMPOSITIONAL DIVERSITY IN THE ATMOSPHERES OF HOT NEPTUNES, WITH APPLICATION TO GJ 436b
Abstract
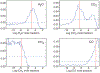
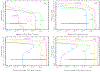
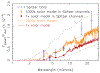
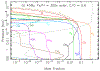
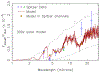
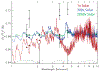
Neptune-sized extrasolar planets that orbit relatively close to their host stars - often called "hot Neptunes" - are common within the known population of exoplanets and planetary candidates. Similar to our own Uranus and Neptune, inefficient accretion of nebular gas is expected produce hot Neptunes whose masses are dominated by elements heavier than hydrogen and helium. At high atmospheric metallicities of 10-10,000× solar, hot Neptunes will exhibit an interesting continuum of atmospheric compositions, ranging from more Neptune-like, H2-dominated atmospheres to more Venus-like, CO2-dominated atmospheres. We explore the predicted equilibrium and disequilibrium chemistry of generic hot Neptunes and find that the atmospheric composition varies strongly as a function of temperature and bulk atmospheric properties such as metallicity and the C/O ratio. Relatively exotic H2O, CO, CO2, and even O2-dominated atmospheres are possible for hot Neptunes. We apply our models to the case of GJ 436b, where we find that a CO-rich, CH4-poor atmosphere can be a natural consequence of a very high atmospheric metallicity. From comparisons of our results with Spitzer eclipse data for GJ 436b, we conclude that although the spectral fit from the high-metallicity forward models is not quite as good as the best fit obtained from pure retrieval methods, the atmospheric composition predicted by these forward models is more physically and chemically plausible in terms of the relative abundance of major constituents. High-metallicity atmospheres (orders of magnitude in excess of solar) should therefore be considered as a possibility for GJ 436b and other hot Neptunes.
Keywords: planetary systems; planets and satellites: atmospheres; planets and satellites: composition; planets and satellites: individual (GJ 436b); stars: individual (GJ 436).
Figures




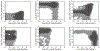



References
-
- Adams ER, Seager S, & Elkins-Tanton L 2008, ApJ, 673, 1160
-
- Agúndez M, Venot O, Iro N, et al. 2012, A&A, 548, A73
-
- Alibert Y, Mordasini C, Benz W, & Winisdoerffer C 2005, A&A, 434, 343
-
- Alibert Y, Baraffe I, Benz W, et al. 2006, A&A, 455, L25
-
- Allard F, Hauschildt PH, Alexander DR, Tamanai A, & Schweitzer A 2001, ApJ, 556, 357
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
