Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Mar 7;19(1):51.
doi: 10.1186/s12874-019-0692-1.

Sample size calculation for estimating key epidemiological parameters using serological data and mathematical modelling

Stéphanie Blaizot  1 , Sereina A Herzog  2   3 , Steven Abrams  4 , Heidi Theeten  5 , Amber Litzroth  6 , Niel Hens  2   4
Affiliations

Sample size calculation for estimating key epidemiological parameters using serological data and mathematical modelling

Stéphanie Blaizot et al. BMC Med Res Methodol. .

Abstract

Background: Our work was motivated by the need to, given serum availability and/or financial resources, decide on which samples to test in a serum bank for different pathogens. Simulation-based sample size calculations were performed to determine the age-based sampling structures and optimal allocation of a given number of samples for testing across various age groups best suited to estimate key epidemiological parameters (e.g., seroprevalence or force of infection) with acceptable precision levels in a cross-sectional seroprevalence survey.

Methods: Statistical and mathematical models and three age-based sampling structures (survey-based structure, population-based structure, uniform structure) were used. Our calculations are based on Belgian serological survey data collected in 2001-2003 where testing was done, amongst others, for the presence of Immunoglobulin G antibodies against measles, mumps, and rubella, for which a national mass immunisation programme was introduced in 1985 in Belgium, and against varicella-zoster virus and parvovirus B19 for which the endemic equilibrium assumption is tenable in Belgium.

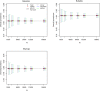
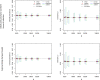
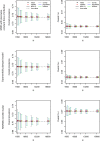
Results: The optimal age-based sampling structure to use in the sampling of a serological survey as well as the optimal allocation distribution varied depending on the epidemiological parameter of interest for a given infection and between infections.

Conclusions: When estimating epidemiological parameters with acceptable levels of precision within the context of a single cross-sectional serological survey, attention should be given to the age-based sampling structure. Simulation-based sample size calculations in combination with mathematical modelling can be utilised for choosing the optimal allocation of a given number of samples over various age groups.

Keywords: Allocation; Infectious diseases; Mathematical models; Precision; Sample size; Study design.

PubMed Disclaimer

Conflict of interest statement

Ethics approval and consent to participate

Ethical approval for the setup of the 2002 serum set was obtained from the Ethics Committee of the University of Antwerp. Since the samples were de-identified, consent was deemed unnecessary according to national regulations (decrees KB 13/02/2001 and KB 17/12/2003).

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Figures

Fig. 1
Fig. 1
Schematic representation of the approach used in this paper
Fig. 2
Fig. 2
Measles, mumps, rubella serological data: mean, median, and 95% confidence interval for the overall seroprevalence over 500 simulations as a function of the total number of sampled individuals (N) using the logistic model with piecewise constant prevalence. Top left: Measles. Top right: Rubella. Bottom: Mumps. “True” overall seroprevalence is the estimated overall seroprevalence using the models on the observed serological survey data (with integer age values). The y-axes have different ranges of values for better legibility
Fig. 3
Fig. 3
Varicella-zoster virus serological data: mean, median, and 95% confidence interval for the overall seroprevalence (left) and overall force of infection (right) over 500 simulations as a function of the total number of sampled individuals (N) for the Maternally-derived immunity-Susceptible-Infectious-Recovered (MSIR) model with piecewise constant force of infection (top) and the exponentially damped model (bottom). “True” overall seroprevalence is the estimated overall seroprevalence using the models on the observed serological survey data (with integer age values)
Fig. 4
Fig. 4
Parvovirus B19 serological data: mean, median, and 95% confidence interval for the overall seroprevalence (left) and overall force of infection (right) over 500 simulations as a function of the total number of sampled individuals (N) for the Maternally-derived immunity-Susceptible-Infectious-Recovered (MSIR) model with piecewise constant force of infection (top), the exponentially damped model (middle), and the MSIR model allowing for age-specific waning of disease-acquired antibodies and boosting of low immunity (MSIRWb-ext AW) model (bottom). “True” overall seroprevalence is the estimated overall seroprevalence using the models on the observed serological data (with integer age values)
Fig. 5
Fig. 5
Optimal allocation (N = 3300) for various epidemiological parameters and by model (y-axis) among the six age groups (with lighter shades with increasing age group): [1,2), [2,6), [6,12), [12,19), [19,31), and [31,65] years, varicella-zoster virus (top) and parvovirus B19 (bottom) serological data. MSIR pcw: MSIR model with piecewise constant force of infection; Exp. damped: exponentially damped model; MSIRWb-ext AW: Maternally-derived immunity-Susceptible-Infectious-Recovered model allowing for age-specific waning of disease-acquired antibodies and boosting of low immunity; f.o.i: force of infection; Prev: prevalence
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Metcalf CJ, Farrar J, Cutts FT, Basta NE, Graham AL, Lessler J, et al. Use of serological surveys to generate key insights into the changing global landscape of infectious disease. Lancet. 2016;388(10045):728–730. doi: 10.1016/S0140-6736(16)30164-7. - DOI - PMC - PubMed
    1. Hens N, Shkedy Z, Aerts M, Faes C, Van Damme P, Beutels P. Modeling infectious disease parameters based on serological and social contact data: a modern statistical perspective. New York: Springer; 2012.
    1. Herzog SA, Blaizot S, Hens N. Mathematical models used to inform study design or surveillance systems in infectious diseases: a systematic review. BMC Infect Dis. 2017;17(1):775. doi: 10.1186/s12879-017-2874-y. - DOI - PMC - PubMed
    1. Marschner IC. Determining the size of a cross-sectional sample to estimate the age-specific incidence of an irreversible disease. Stat Med. 1994;13(22):2369–2381. doi: 10.1002/sim.4780132208. - DOI - PubMed
    1. Keiding N. Age-specific incidence and prevalence - a statistical perspective. J R Stat Soc Ser A Stat Soc. 1991;154:371–412. doi: 10.2307/2983150. - DOI

Publication types

MeSH terms

Substances