Eukaryotic Cell Dynamics from Crawlers to Swimmers
- PMID: 30854030
- PMCID: PMC6402608
- DOI: 10.1002/wcms.1376
Eukaryotic Cell Dynamics from Crawlers to Swimmers
Abstract
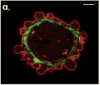
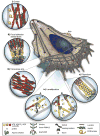
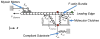
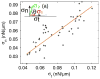
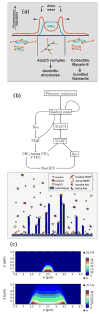
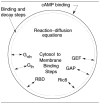
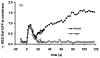
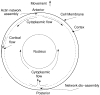
Movement requires force transmission to the environment, and motile cells are robustly, though not elegantly, designed nanomachines that often can cope with a variety of environmental conditions by altering the mode of force transmission used. As with humans, the available modes range from momentary attachment to a substrate when crawling, to shape deformations when swimming, and at the cellular level this involves sensing the mechanical properties of the environment and altering the mode appropriately. While many types of cells can adapt their mode of movement to their microenvironment (ME), our understanding of how they detect, transduce and process information from the ME to determine the optimal mode is still rudimentary. The shape and integrity of a cell is determined by its cytoskeleton (CSK), and thus the shape changes that may be required to move involve controlled remodeling of the CSK. Motion in vivo is often in response to extracellular signals, which requires the ability to detect such signals and transduce them into the shape changes and force generation needed for movement. Thus the nanomachine is complex, and while much is known about individual components involved in movement, an integrated understanding of motility in even simple cells such as bacteria is not at hand. In this review we discuss recent advances in our understanding of cell motility and some of the problems remaining to be solved.
Figures






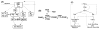





References
-
- Nürnberg A, Kitzing T, Grosse R. Nucleating actin for invasion. Nature Reviews Cancer. 2011;11(3):177–187. - PubMed
-
- Haeger A, Wolf K, Zegers MM, Friedl P. Collective cell migration: guidance principles and hierarchies. Trends in cell biology. 2015;25(9):556–566. - PubMed
-
- Boekhorst VT, Preziosi L, Friedl P. Plasticity of cell migration in vivo and in silico. Annual review of cell and developmental biology. 2016;32:491–526. - PubMed
-
- Ridley AJ. Life at the leading edge. Cell. 2011;145(7):1012–1022. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
