Latent goal models for dynamic strategic interaction
- PMID: 30856172
- PMCID: PMC6472832
- DOI: 10.1371/journal.pcbi.1006895
Latent goal models for dynamic strategic interaction
Abstract
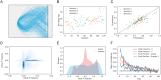
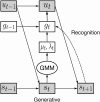
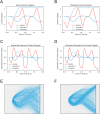
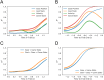
Understanding the principles by which agents interact with both complex environments and each other is a key goal of decision neuroscience. However, most previous studies have used experimental paradigms in which choices are discrete (and few), play is static, and optimal solutions are known. Yet in natural environments, interactions between agents typically involve continuous action spaces, ongoing dynamics, and no known optimal solution. Here, we seek to bridge this divide by using a "penalty shot" task in which pairs of monkeys competed against each other in a competitive, real-time video game. We modeled monkeys' strategies as driven by stochastically evolving goals, onscreen positions that served as set points for a control model that produced observed joystick movements. We fit this goal-based dynamical system model using approximate Bayesian inference methods, using neural networks to parameterize players' goals as a dynamic mixture of Gaussian components. Our model is conceptually simple, constructed of interpretable components, and capable of generating synthetic data that capture the complexity of real player dynamics. We further characterized players' strategies using the number of change points on each trial. We found that this complexity varied more across sessions than within sessions, and that more complex strategies benefited offensive players but not defensive players. Together, our experimental paradigm and model offer a powerful combination of tools for the study of realistic social dynamics in the laboratory setting.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

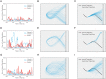

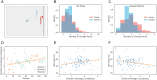
References
-
- Dunbar R. The social brain hypothesis. brain. 1998;9(10):178–190.
-
- Camerer C. Behavioral game theory: Experiments in strategic interaction. Princeton University Press; 2003.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

