Boosting Rechargeable Batteries R&D by Multiscale Modeling: Myth or Reality?
- PMID: 30859816
- PMCID: PMC6460402
- DOI: 10.1021/acs.chemrev.8b00239
Boosting Rechargeable Batteries R&D by Multiscale Modeling: Myth or Reality?
Abstract
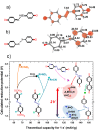
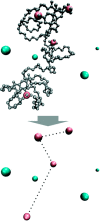
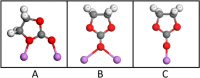
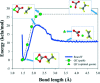
This review addresses concepts, approaches, tools, and outcomes of multiscale modeling used to design and optimize the current and next generation rechargeable battery cells. Different kinds of multiscale models are discussed and demystified with a particular emphasis on methodological aspects. The outcome is compared both to results of other modeling strategies as well as to the vast pool of experimental data available. Finally, the main challenges remaining and future developments are discussed.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
























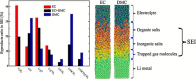



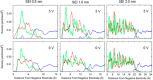






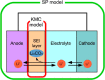



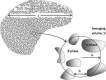
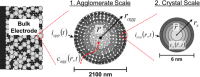








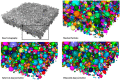

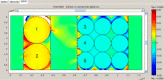

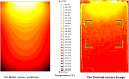

References
-
- The Latest Bull Case for Electric Cars: The Cheapest Batteries Ever. Bloomberg.com. December 5, 2017.
-
- Blomgren G. E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2017, 164, A5019–A5025. 10.1149/2.0251701jes. - DOI
-
- Franco A.Rechargeable Lithium Batteries: From Fundamentals to Applications; Elsevier, 2015.
-
- Theory: Definition of theory in English by Oxford Dictionaries. https://en.oxforddictionaries.com/definition/theory (accessed Aug 22, 2018).
-
- Franco A. A. Multiscale Modelling and Numerical Simulation of Rechargeable Lithium Ion Batteries: Concepts, Methods and Challenges. RSC Adv. 2013, 3, 13027–13058. 10.1039/c3ra23502e. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

