Spike burst-pause dynamics of Purkinje cells regulate sensorimotor adaptation

Abstract

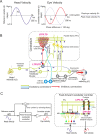
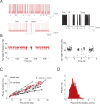
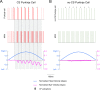
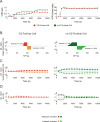
Cerebellar Purkinje cells mediate accurate eye movement coordination. However, it remains unclear how oculomotor adaptation depends on the interplay between the characteristic Purkinje cell response patterns, namely tonic, bursting, and spike pauses. Here, a spiking cerebellar model assesses the role of Purkinje cell firing patterns in vestibular ocular reflex (VOR) adaptation. The model captures the cerebellar microcircuit properties and it incorporates spike-based synaptic plasticity at multiple cerebellar sites. A detailed Purkinje cell model reproduces the three spike-firing patterns that are shown to regulate the cerebellar output. Our results suggest that pauses following Purkinje complex spikes (bursts) encode transient disinhibition of target medial vestibular nuclei, critically gating the vestibular signals conveyed by mossy fibres. This gating mechanism accounts for early and coarse VOR acquisition, prior to the late reflex consolidation. In addition, properly timed and sized Purkinje cell bursts allow the ratio between long-term depression and potentiation (LTD/LTP) to be finely shaped at mossy fibre-medial vestibular nuclei synapses, which optimises VOR consolidation. Tonic Purkinje cell firing maintains the consolidated VOR through time. Importantly, pauses are crucial to facilitate VOR phase-reversal learning, by reshaping previously learnt synaptic weight distributions. Altogether, these results predict that Purkinje spike burst-pause dynamics are instrumental to VOR learning and reversal adaptation.

Fig 1. Vestibular ocular reflex (VOR) and cerebellar control loop.

(A) Horizontal VOR (h-VOR) protocols compare head rotational movements (input) against the induced contralateral eye movements (output) via two measurements: the VOR gain, i.e. the ratio between eye and head speeds (E_v and H_v, respectively); and the VOR phase, i.e. the temporal lag between eye and head velocity signals. (B) Schematic representation of the main neural layers, cells, connections, and plasticity sites considered in the cerebellar model. Mossy fibres (MFs) convey the sensory signals from the vestibular organ and they provide the input to the cerebellar network. MFs project sensorimotor information onto granular cells (GCs) and medial vestibular nuclei (MVN). GCs, in turn, project onto Purkinje cells through parallel fibres (PFs). Purkinje cells also receive excitatory inputs from the climbing fibres (CFs). CFs deliver the error signals encoding instructive terms that drive motor control learning. Purkinje cells integrate CF and PF inputs, thus transmitting the difference between head and eye movements. Finally, MVN are inhibited by Purkinje cells and provide the main cerebellar output. The cerebellar model implements different spike timing dependent plasticity mechanisms at multiple sites: PF-Purkinje cell, MF-MVN, and Purkinje cell-MVN synapses. (C) Cerebellar feed-forward control system comparing a known reference (head velocity or input variable) to the actual output (eye velocity) to quantify an error signal, whose delay matches the sensory-motor pathway delay (~100 ms) [7]. The cerebellum compensates for the difference between actual eye (represented as an inverter logic gate in this scheme) and head velocity profiles. The head velocity consists of a 1 Hz sinusoidal function iteratively presented to the cerebellar model, mimicking the sinusoidal frequency of the head rotation in experimental protocols [8].

Fig 2. Spike burst–pause properties of model Purkinje cell responses.

(A) Simulated (left) and electrophysiological (right) recordings of Purkinje cell spike outputs in response to CF spike excitatory postsynaptic potentials occurring at physiological frequencies (arrows) (data from [41]). CF discharges trigger transitions between Purkinje cell Na⁺ spike output and CF-evoked bursts and pauses via complex spikes. Here, the Purkinje cell model was run on the EDLUT simulator (see Methods). (B) Simulated (left) and experimental (right) Purkinje cell tonic spike frequency during CF discharges aligned with spike-grams in A (data from [41]). N = 10 Purkinje cells were simulated to compute the tonic spike frequency. (C) Relation between pause duration and pre-complex spike (pre–CS) inter spike intervals (ISIs) when increasing the amplitude of the injected current: model data (red circles, n = 1000) vs. experimental data [44] (grey to black dots). Grey-to-black lines represent individual cells (n = 10). The blue dashed line is the linear regression curve fitting model data. The model captures the relation between spike pause duration and pre-complex spike ISI duration observed electro physiologically [44]. (D) Distribution of ISI values following the complex spike (post-CS). The ISI duration is normalised to pre-CS ISI values. The Kurtosis for the distribution of post-CS ISI values is 4.24. The skewness is positive (0.6463), thus indicating an asymmetric post-CS ISI distribution. Kurtosis and skewness values were consistent with Purkinje cell data [44].

Fig 3. Purkinje post–complex spike pauses act as a gating mechanism for early coarse VOR in the absence of cerebellar adaptation.

Only half of h-VOR cycle is represented. Two equal cerebellar network configurations except for the Purkinje cell dynamics were compared under equal stimulation. (A) The first model accounts for CF-evoked Purkinje spike burst-pause dynamics. CF stimulation generates complex spikes and subsequent post–complex spike pauses. The latter allows MFs to drive directly the immediate activation of MVN, which facilitates an early but rough eye movement compensation for head velocity. (B) The second model only exhibits Purkinje tonic firing (i.e., complex spiking is blocked through the blockade of muscarinic voltage-dependent channels, see Methods), which prevents MFs from eliciting any baseline MVN compensatory output. See S2 and S3 Figs for a sensitivity analysis of parameters regulating the LTD/LTP balance at PF-Purkinje cell and MF-MVN synapses. See also S4 Fig for the same parameter sensitivity analysis in the absence of Purkinje spike burst-pause dynamics.

Fig 4. Role of Purkinje spike burst-pause dynamics in VOR cerebellar adaptation.

(A) VOR gain and phase adaptation with (purple curve) and without (green curve) CF-evoked Purkinje spike burst-pause dynamics. VOR cerebellar adaptation starts with zero gain owing to the initial synaptic weights at PF and MVN afferents (Table 5). Purkinje spike burst-pause dynamics provides better VOR gain adaptation (in terms of both rate and precision) converging to gain values within [0.8–0.9] (S5 Fig), which are consistent with experimental data [40, 45, 46]. (B) Purkinje complex spiking allows a sparser weight distribution (with higher Kurtosis) to be learnt at MF-MVN synapses, with significantly lesser MF afferents needed for learning consolidation. (C) The model endowed with Purkinje complex spiking updates less MF afferents during learning consolidation but their synaptic range is fully exploited. (D) The averaged synaptic weight variations are more selective during the adaptive process in the presence of Purkinje spike burst-pause dynamics, yet the standard deviation remains equal.

Fig 5. Purkinje spike burst-pause dynamics facilitates VOR phase-reversal learning.

(A) VOR gain adaptation with (red curve) and without (green curve) Purkinje spike burst-pause dynamics during: VOR adaptation (first 10000 s), phase-reversal learning (subsequent 12000 s), and normal VOR restoration (remaining 12000 s). (B) Purkinje spike burst-pause dynamics provides fast learning reversibility, consistently with experimental recordings [2]. By contrast, phase-reversal VOR learning is impaired in the absence of Purkinje complex spiking. See S6 Fig for the time course of VOR phase-reversal learning.

Fig 6. Evolution of synaptic weight distributions during VOR phase-reversal learning.

(A) Only the sparser and more selective distribution of MF-MVN synaptic weights resulting from the interplay between bursts and post-complex spike pauses facilitates an efficient reshaping of the learnt patterns (B), allowing phase-reversal learning to be achieved (C).

Fig 7. LTP blockades (due to dominant LTD) during REMs explain reversal VOR gain discontinuities between training sessions.

We simulated 6 REMs stages (for a total of 18000 s of simulation) between day 1 and 2 of VOR phase-reversal learning. High levels of MF activity (10 Hz) leads to a dominance of LTP at both PF-Purkinje cell and MF-MVN synapses during REMs. Hence, during REMs the cerebellar model keeps ‘forgetting’ the memory traces as during day 1 (blue curve). A smaller MF activity (2.5 Hz) leads to a balance of LTP (driven by vestibular activity) and LTD (driven by the CFs). Thus, the model tends to maintain the synaptic weights learnt during day 1 (green curve). A very low MF activity (1 Hz) makes LTD to block LTP at PF-Purkinje and MF-MVN synapses. Under this third hypothesis, the synaptic weights tend to decay back towards their initial value (red curve) in accordance with experimental data [2] (black curve). See S9 Fig for the modelled probabilistic Poisson process underpinning CF activation.

Fig 8. Purkinje complex spike-pause frequency and VOR gain error during adaptation and post/pre adaptation.

The frequency of Purkinje complex spike-pauses (red squares) diminishes through VOR adaptation from 8–9 Hz to 2–3 Hz under a sinusoidal vestibular stimulus of ~1 Hz. After VOR adaptation, a direct random stimulation of CFs at 7 Hz during 30 min as in [50] impairs the VOR reflex. The evolution of the VOR gain error (Mean Absolute Error; black curve) during adaptation, post-adaptation, and artificial random stimulation of CFs.