Predicting Brain Age Based on Spatial and Temporal Features of Human Brain Functional Networks
- PMID: 30863296
- PMCID: PMC6399206
- DOI: 10.3389/fnhum.2019.00062
Predicting Brain Age Based on Spatial and Temporal Features of Human Brain Functional Networks
Abstract
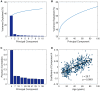
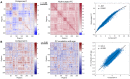
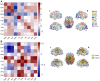
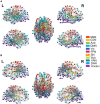
The organization of human brain networks can be measured by capturing correlated brain activity with functional MRI data. There have been a variety of studies showing that human functional connectivities undergo an age-related change over development. In the present study, we employed resting-state functional MRI data to construct functional network models. Principal component analysis was performed on the FC matrices across all the subjects to explore meaningful components especially correlated with age. Coefficients across the components, edge features after a newly proposed feature reduction method as well as temporal features based on fALFF, were extracted as predictor variables and three different regression models were learned to make prediction of brain age. We observed that individual's functional network architecture was shaped by intrinsic component, age-related component and other components and the predictive models extracted sufficient information to provide comparatively accurate predictions of brain age.
Keywords: fMRI; functional connectivity; lifespan; predictive model; principal component; resting state.
Figures
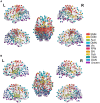

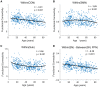
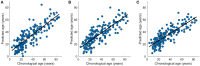
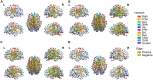
References
-
- Battaglia D., Thomas B., Hansen E. C., Chettouf S., Daffertshofer A., McIntosh A. R., et al. (2017). Functional connectivity dynamics of the resting state across the human adult lifespan. bioRxiv 107243 10.1101/107243 - DOI
LinkOut - more resources
Full Text Sources

