SANTA-SIM: simulating viral sequence evolution dynamics under selection and recombination
- PMID: 30863552
- PMCID: PMC6407609
- DOI: 10.1093/ve/vez003
SANTA-SIM: simulating viral sequence evolution dynamics under selection and recombination
Abstract
Simulations are widely used to provide expectations and predictive distributions under known conditions against which to compare empirical data. Such simulations are also invaluable for testing and comparing the behaviour and power of inference methods. We describe SANTA-SIM, a software package to simulate the evolution of a population of gene sequences forwards through time. It models the underlying biological processes as discrete components: replication, recombination, point mutations, insertion-deletions, and selection under various fitness models and population size dynamics. The software is designed to be intuitive to work with for a wide range of users and executable in a cross-platform manner.
Keywords: fitness; mutation; recombination; selection; simulation.
Figures
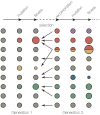
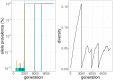
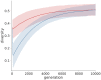
References
-
- Balloux F. (2001) ‘EASYPOP (version 1.7): A Computer Program for Population Genetics Simulations’, The Journal of Heredity, 92: 301–2. - PubMed
-
- Gillespie J. H. (2001) ‘Is the Population Size of a Species Relevant to Its Evolution?’, Evolution; International Journal of Organic Evolution, 55: 2161–9. - PubMed
-
- Guillaume F., Rougemont J. (2006) ‘Nemo: An Evolutionary and Population Genetics Programming Framework’, Bioinformatics, 22: 2556–7. - PubMed
-
- Haller B. C., Messer P. W. (2017) ‘SLiM 2: Flexible, Interactive Forward Genetic Simulations’, Molecular Biology and Evolution, 34: 230–40. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources

