Physics of growing biological tissues: the complex cross-talk between cell activity, growth and resistance

Abstract

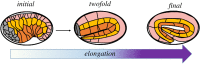
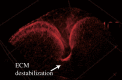
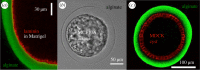
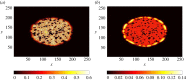
For many organisms, shapes emerge from growth, which generates stresses, which in turn can feedback on growth. In this review, theoretical methods to analyse various aspects of morphogenesis are discussed with the aim to determine the most adapted method for tissue mechanics. We discuss the need to work at scales intermediate between cells and tissues and emphasize the use of finite elasticity for this. We detail the application of these ideas to four systems: active cells embedded in tissues, brain cortical convolutions, the cortex of Caenorhabditis elegans during elongation and finally the proliferation of epithelia on extracellular matrix. Numerical models well adapted to inhomogeneities are also presented. This article is part of the theme issue 'Rivlin's legacy in continuum mechanics and applied mathematics'.

Keywords: active and multi-scale rheology; finite elasticity; morphogenesis; tissue growth; tissue mechanics.

Figure 1.

From [68], (a) collagen network within a Baker II capsule (Baker grade indicates the degree of the pathology, Baker II being an intermediate level of pathology). The green birefringence shows the loose organization of collagen fibres wrapped around tighter organized collagen fibres in red. (b) Periodic spacing of collagen fibres making up the thick cables in Baker III capsules. (c) Cells aligned parallel to the collagen fibres in Baker II capsules. (Online version in colour.)

Figure 2.

(a) ‘Cigar shaped’ configurations of tumour cell nuclei of a leiomyosarcoma with nuclear atypia [74]. (b) Histological appearance of a leiomyosarcoma after resection of a tumour in the subclavicular region [75]. (Online version in colour.)

Figure 3.

Embryonic elongation in C. elegans is driven in part by epidermal actomyosin contractility and in part by muscle contraction. Inspired by [14]. In pink, the dorsal epithelial cells, in yellow the seam epithelial cells, in orange the ventral cells. (Online version in colour.)

Figure 4.

Generation of buckling-like three-dimensional shapes through localized destabilization of ECM after expression of the protease Mmp2 in a central band of the tissue, leading to a deep fold in the tissue (exact genotype: ubi-cad:GFP Gal80ts; UAS-Mmp2/DppGal4).

Figure 5.

(a) Confocal section of an alginate capsule (green) coated with a layer of ECM (red); (b) Phase contrast videomicrograph of an encapsulated cyst of MCF10A (epithelial cell from the mammary gland); (c) Confocal equatorial section of an MDCK cyst (red) in an alginate capsule (green).

Figure 6.

Distribution of cells computed with the two-dimensional mixture model including cancer stem cells, differentiated cells and inert cells (dead, of different type such as blood cells). The computation was seeded from a small number of cells. (a) Differentiated cell distribution. (b) Cancer stem cell distribution. The black dots represent obstacles (vessels, fibres). This numerical computation includes a chemical signal exchange in between cells (such as growth factors) and growth feedback control loops (unpublished preliminary data [127]). (Online version in colour.)