Incorporating prior knowledge via volumetric deep residual network to optimize the reconstruction of sparsely sampled MRI
- PMID: 30880112
- PMCID: PMC6745016
- DOI: 10.1016/j.mri.2019.03.012
Incorporating prior knowledge via volumetric deep residual network to optimize the reconstruction of sparsely sampled MRI
Abstract
For sparse sampling that accelerates magnetic resonance (MR) image acquisition, non-linear reconstruction algorithms have been developed, which incorporated patient specific a prior information. More generic a prior information could be acquired via deep learning and utilized for image reconstruction. In this study, we developed a volumetric hierarchical deep residual convolutional neural network, referred to as T-Net, to provide a data-driven end-to-end mapping from sparsely sampled MR images to fully sampled MR images, where cartilage MR images were acquired using an Ultra-short TE sequence and retrospectively undersampled using pseudo-random Cartesian and radial acquisition schemes. The network had a hierarchical architecture that promoted the sparsity of feature maps and increased the receptive field, which were valuable for signal synthesis and artifact suppression. Relatively dense local connections and global shortcuts were established to facilitate residual learning and compensate for details lost in hierarchical processing. Additionally, volumetric processing was adopted to fully exploit spatial continuity in three-dimensional space. Data consistency was further enforced. The network was trained with 336 three-dimensional images (each consisting of 32 slices) and tested by 24 images. The incorporation of a priori information acquired via deep learning facilitated high acceleration factors (as high as 8) while maintaining high image fidelity (quantitatively evaluated using the structural similarity index measurement). The proposed T-Net had an improved performance as compared to several state-of-the-art networks.
Copyright © 2019 Elsevier Inc. All rights reserved.
Figures
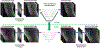








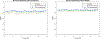



References
-
- Lustig M, Donoho D, and Pauly JM, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic resonance in medicine, vol. 58, pp. 1182–1195, 2007. - PubMed
-
- Qu X, Cao X, Guo D, Hu C, and Chen Z, “Combined sparsifying transforms for compressed sensing MRI,” Electronics letters, vol. 46, pp. 121–123, 2010.
-
- Lai Z, Qu X, Liu Y, Guo D, Ye J, Zhan Z, et al., “Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform,” Medical image analysis, vol. 27, pp. 93–104, 2016. - PubMed
-
- Ravishankar S and Bresler Y, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” IEEE transactions on medical imaging, vol. 30, p. 1028, 2011. - PubMed
-
- Huang Y, Paisley J, Lin Q, Ding X, Fu X, and Zhang X-P, “Bayesian nonparametric dictionary learning for compressed sensing MRI,” IEEE Transactions on Image Processing, vol. 23, pp. 5007–5019, 2014. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

