Multicompartment Magnetic Resonance Fingerprinting
- PMID: 30880863
- PMCID: PMC6415771
- DOI: 10.1088/1361-6420/aad1c3
Multicompartment Magnetic Resonance Fingerprinting
Abstract
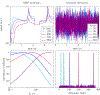
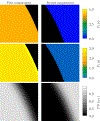
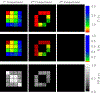
Magnetic resonance fingerprinting (MRF) is a technique for quantitative estimation of spin- relaxation parameters from magnetic-resonance data. Most current MRF approaches assume that only one tissue is present in each voxel, which neglects intravoxel structure, and may lead to artifacts in the recovered parameter maps at boundaries between tissues. In this work, we propose a multicompartment MRF model that accounts for the presence of multiple tissues per voxel. The model is fit to the data by iteratively solving a sparse linear inverse problem at each voxel, in order to express the measured magnetization signal as a linear combination of a few elements in a precomputed fingerprint dictionary. Thresholding-based methods commonly used for sparse recovery and compressed sensing do not perform well in this setting due to the high local coherence of the dictionary. Instead, we solve this challenging sparse-recovery problem by applying reweighted-𝓁1-norm regularization, implemented using an efficient interior-point method. The proposed approach is validated with simulated data at different noise levels and undersampling factors, as well as with a controlled phantom-imaging experiment on a clinical magnetic-resonance system.
Keywords: Quantitative MRI; coherent dictionaries; magnetic resonance fingerprinting; multicompartment models; parameter estimation; reweighted 𝓁1 -norm; sparse recovery.
Figures













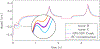


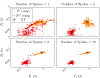

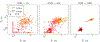





References
-
- Allerhand A and Gutowsky HS. Spin-Echo NMR Studies of Chemical Exchange. I. Some General Aspects. The Journal of Chemical Physics, 41:2115–2126, Oct. 1964. - PubMed
-
- Assländer J, Glaser SJ, and Hennig J. Pseudo steady-state free precession for mr-fingerprinting. Magnetic resonance in medicine, 77(3):1151–1161, 2017. - PubMed
-
- Assländer J, Lattanzi R, Sodickson DK, and Cloos MA. Relaxation in Spherical Coordinates: Analysis and Optimization of pseudo-SSFP based MR-Fingerprinting. arXiv, 1703.00481(v1), 2017.
-
- Beck A and Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences, 2(1):183–202, 2009.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
