Simulations of Protein Adsorption on Nanostructured Surfaces

Abstract

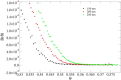
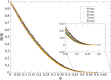
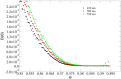
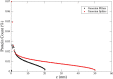
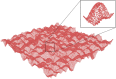
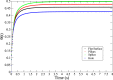
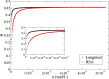
Recent technological advances have allowed the development of a new generation of nanostructured materials, such as those displaying both mechano-bactericidal activity and substrata that favor the growth of mammalian cells. Nanomaterials that come into contact with biological media such as blood first interact with proteins, hence understanding the process of adsorption of proteins onto these surfaces is highly important. The Random Sequential Adsorption (RSA) model for protein adsorption on flat surfaces was modified to account for nanostructured surfaces. Phenomena related to the nanofeature geometry have been revealed during the modelling process; e.g., convex geometries can lead to lower steric hindrance between particles, and hence higher degrees of surface coverage per unit area. These properties become more pronounced when a decrease in the size mismatch between the proteins and the surface nanostructures occurs. This model has been used to analyse the adsorption of human serum albumin (HSA) on a nano-structured black silicon (bSi) surface. This allowed the Blocking Function (the rate of adsorption) to be evaluated. The probability of the protein to adsorb as a function of the occupancy was also calculated.

Figure 1

Comparison of sphere occupancy in one dimension on a flat surface and on a spherical shell. The given length L of the segment in the upper case (flat substrate) corresponds to 2L = πD in the lower case (curved substrate), where D is the diameter of the hemisphere. In both figures, the small spheres have identical diameters, but in the second case the occupancy θ is larger.

Figure 2

Intermediate (a) and final (b–d) configuration for RSA simulations of four different surfaces: (a) Flat surface, (b) Gaussian pillar with W = 80 nm and H = 200 nm (Psaltoda claripennis model), (c) Gaussian spike with W = 60 nm and H = 500 nm (bSi model) and (d) Gaussian “hole” with W = 60 nm and H = −550 nm. This snapshots have been obtained using OVITO.

Figure 3

Blocking function B(θ) for: flat surface (black), Gaussian pillars (red), Gaussian spikes (green) and Gaussian hole (blue) defined by Equation (4). The inset highlights the ending points corresponding to θ_∞.

Figure 4

Blocking function of pillars using different widths at fixed height (200 nm).

Figure 5

Blocking function of pillars using different heights at fixed width (80 nm).

Figure 6

Blocking function of spikes using different widths at fixed height (500 nm). The isolated points are due to fluctuations in the statistical sampling.

Figure 7

Blocking function of spikes using different heights at fixed width (60 nm). The isolated points are due to fluctuations in the statistical sampling.

Figure 8

θ_∞ as a function of 1/W (i.e. the curvature) for both Gaussian pillars (black) and Gaussian spikes (red). The lines represent a linear fit, demonstrating a linear increase with increase of curvature.

Figure 9

Vertical distribution of proteins for Gaussian pillars with W = 80 nm and H = 200 nm, and for Gaussian spikes with W = 60 nm and H = 500 nm. The number of proteins adsorbing on the bottom of the pillars is clearly much greater than that on the top of the pillars, a consequence of lower surface availability. The discontinuity in the left-hand side figure is a simple consequence of the definition of the shape, Eq. 4.

Figure 10

Saturation limit of RSA simulation of albumin adsorption onto a bSi surface represented by an AFM scan.

Figure 11

Blocking function of albumin adsorption on the AFM scan of the real bSi surface.

Figure 12

Coverage as a function of time for the four surfaces investigated (n = 1.06⋅10⁻⁵ mol/L).

Figure 13

Coverage as a function of time for the four surfaces investigated (n = 5.3 ⋅ 10⁻⁴ mol/L).

Figure 14

Langmuir adsorption isotherms on flat (black) and nanostructured surface composed of cylinders (red).

Figure 15

RSA isotherm (red) in comparison with the Langmuir isotherm (black) for spherical proteins adsorbing onto a flat surface.