Self-organized mechano-chemical dynamics in amoeboid locomotion of Physarum fragments
- PMID: 30906070
- PMCID: PMC6430145
- DOI: 10.1088/1361-6463/aa68be
Self-organized mechano-chemical dynamics in amoeboid locomotion of Physarum fragments
Abstract
The aim of this work is to quantify the spatio-temporal dynamics of flow-driven amoeboid locomotion in small (~100 µm) fragments of the true slime mold Physarum polycephalum. In this model organism, cellular contraction drives intracellular flows, and these flows transport the chemical signals that regulate contraction in the first place. As a consequence of these non-linear interactions, a diversity of migratory behaviors can be observed in migrating Physarum fragments. To study these dynamics, we measure the spatio-temporal distributions of the velocities of the endoplasm and ectoplasm of each migrating fragment, the traction stresses it generates on the substratum, and the concentration of free intracellular calcium. Using these unprecedented experimental data, we classify migrating Physarum fragments according to their dynamics, finding that they often exhibit spontaneously coordinated waves of flow, contractility and chemical signaling. We show that Physarum fragments exhibiting symmetric spatio-temporal patterns of endoplasmic flow migrate significantly slower than fragments with asymmetric patterns. In addition, our joint measurements of ectoplasm velocity and traction stress at the substratum suggest that forward motion of the ectoplasm is enabled by a succession of stick-slip transitions, which we conjecture are also organized in the form of waves. Combining our experiments with a simplified convection-diffusion model, we show that the convective transport of calcium ions may be key for establishing and maintaining the spatiotemporal patterns of calcium concentration that regulate the generation of contractile forces.
Keywords: amoeboid motility; cell migration; mechano-chemical interactions; particle image velocimetry; physarum; traction force microscopy.
Figures
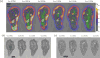


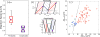
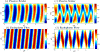
 , peristaltic fragments;
, peristaltic fragments;
 , amphistaltic fragments. The dashed line is Δxcent = Δxflow.
, amphistaltic fragments. The dashed line is Δxcent = Δxflow.
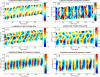

 ) and longitudinal traction stresses (
) and longitudinal traction stresses (
 ) at two specific locations in the front (panel a) and the back (panel b) of the peristaltic Physarum fragment shown in Figure 7. The tiled bars at the top of the plots represent the time-dependent phase differences (in radians) between the ectoplasm velocity and the traction stresses. Blue and orange tiles represent phase differences near −π/2 (cell and substrate stick) and zero (cell and substrate slip) respectively, as indicated by the color scale at the top of the figure.
) at two specific locations in the front (panel a) and the back (panel b) of the peristaltic Physarum fragment shown in Figure 7. The tiled bars at the top of the plots represent the time-dependent phase differences (in radians) between the ectoplasm velocity and the traction stresses. Blue and orange tiles represent phase differences near −π/2 (cell and substrate stick) and zero (cell and substrate slip) respectively, as indicated by the color scale at the top of the figure.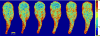
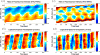

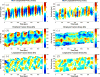
 ) and ratiometric measurement of [Ca2+]i (
) and ratiometric measurement of [Ca2+]i (
 ), averaged along the width of a peristaltic fragment (panels a and c) and an amphistaltic fragment (panels e and g). Bottom row (b, d, f, h): Time histories of endoplasmic flow velocity (
), averaged along the width of a peristaltic fragment (panels a and c) and an amphistaltic fragment (panels e and g). Bottom row (b, d, f, h): Time histories of endoplasmic flow velocity (
 ) and peripheral traction stress (
) and peripheral traction stress (
 ), averaged along the width of a peristaltic fragment (panels b and d) and an amphistaltic fragment (panels f and h). Panels (a, b, e, f): Fragment front. Panels (c, d, g, h): Fragment rear.
), averaged along the width of a peristaltic fragment (panels b and d) and an amphistaltic fragment (panels f and h). Panels (a, b, e, f): Fragment front. Panels (c, d, g, h): Fragment rear.Similar articles
-
Coordination of contractility, adhesion and flow in migrating Physarum amoebae.J R Soc Interface. 2015 May 6;12(106):20141359. doi: 10.1098/rsif.2014.1359. J R Soc Interface. 2015. PMID: 25904525 Free PMC article.
-
Periodic traction in migrating large amoeba of Physarum polycephalum.J R Soc Interface. 2015 May 6;12(106):20150099. doi: 10.1098/rsif.2015.0099. J R Soc Interface. 2015. PMID: 25808339 Free PMC article.
-
Spatio-temporal relationships between protoplasmic streaming and contraction activities in plasmodial veins of Physarum polycephalum.Cytobiologie. 1978 Aug;17(2):317-34. Cytobiologie. 1978. PMID: 689259
-
Intelligent behaviors of amoeboid movement based on complex dynamics of soft matter.Soft Matter. 2007 Dec 11;4(1):57-67. doi: 10.1039/b706317m. Soft Matter. 2007. PMID: 32907084 Review.
-
Fluid flows shaping organism morphology.Philos Trans R Soc Lond B Biol Sci. 2018 May 26;373(1747):20170112. doi: 10.1098/rstb.2017.0112. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 29632264 Free PMC article. Review.
Cited by
-
A lumped parameter model of endoplasm flow in Physarum polycephalum explains migration and polarization-induced asymmetry during the onset of locomotion.PLoS One. 2019 Apr 23;14(4):e0215622. doi: 10.1371/journal.pone.0215622. eCollection 2019. PLoS One. 2019. PMID: 31013306 Free PMC article.
-
Dynamics of centipede locomotion revealed by large-scale traction force microscopy.J R Soc Interface. 2024 May;21(214):20230439. doi: 10.1098/rsif.2023.0439. Epub 2024 May 29. J R Soc Interface. 2024. PMID: 38807527 Free PMC article.
-
Active poroelastic two-phase model for the motion of physarum microplasmodia.PLoS One. 2019 Aug 9;14(8):e0217447. doi: 10.1371/journal.pone.0217447. eCollection 2019. PLoS One. 2019. PMID: 31398215 Free PMC article.
-
Oscillatory fluid flow drives scaling of contraction wave with system size.Proc Natl Acad Sci U S A. 2018 Oct 16;115(42):10612-10617. doi: 10.1073/pnas.1805981115. Epub 2018 Oct 3. Proc Natl Acad Sci U S A. 2018. PMID: 30282737 Free PMC article.
-
Encoding memory in tube diameter hierarchy of living flow network.Proc Natl Acad Sci U S A. 2021 Mar 9;118(10):e2007815118. doi: 10.1073/pnas.2007815118. Proc Natl Acad Sci U S A. 2021. PMID: 33619174 Free PMC article.
References
-
- Charras G, Paluch E. Blebs Lead the Way: How to Migrate Without Lamellipodia. Nature Reviews: Molecular Cell Biology. 2008 Sep;9(9):730–736. - PubMed
-
- Lämmermann T, Bader BL, Monkley SJ, Worbs T, Wedlich-Söldner R, Hirsch K, et al. Rapid Leukocyte Migration by Integrin-Independent Flowing and Squeezing. Nature. 2008 May;453(7191):51–55. - PubMed
-
- Yoshida K, Soldati T. Dissection of amoeboid movement into two mechanically distinct modes. Journal of cell science. 2006;119(18):3833–3844. - PubMed
-
- Piovanelli M, Fujie T, Mazzolai B, Beccai L. Biomedical Robotics and Biomechatronics, the IEEE RAS EMBS International Conference on. IEEE; 2012. A Bio-Inspired Approach Towards the Development of Soft Amoeboid Microrobots; pp. 612–616.
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
