Drug Delivery From Polymer-Based Nanopharmaceuticals-An Experimental Study Complemented by Simulations of Selected Diffusion Processes

Abstract

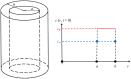
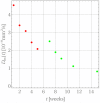
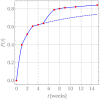
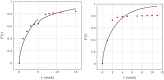
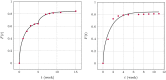
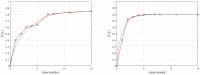
The success of medical therapy depends on the correct amount and the appropriate delivery of the required drugs for treatment. By using biodegradable polymers a drug delivery over a time span of weeks or even months is made possible. This opens up a variety of strategies for better medication. The drug is embedded in a biodegradable polymer (the "carrier") and injected in a particular position of the human body. As a consequence of the interplay between the diffusion process and the degrading polymer the drug is released in a controlled manner. In this work we study the controlled release of medication experimentally by measuring the delivered amount of drug within a cylindrical shell over a long time interval into the body fluid. Moreover, a simple continuum model of the Fickean type is initially proposed and solved in closed-form. It is used for simulating some of the observed release processes for this type of carrier and takes the geometry of the drug container explicitly into account. By comparing the measurement data and the model predictions diffusion coefficients are obtained. It turns out that within this simple model the coefficients change over time. This contradicts the idea that diffusion coefficients are constants independent of the considered geometry. The model is therefore extended by taking an additional absorption term into account leading to a concentration dependent diffusion coefficient. This could now be used for further predictions of drug release in carriers of different shape. For a better understanding of the complex diffusion and degradation phenomena the underlying physics is discussed in detail and even more sophisticated models involving different degradation and mass transport phenomena are proposed for future work and study.

Keywords: biphosphonate; diffusion coefficient; gentamicin; modeling; polylacetic acid.

Figure 1

Left: Film matrix specimens before and after curling; Right: specimens in a tube.

Figure 2

SEM of the drug containment.

Figure 3

Fractional cumulative release of GM from PLA thin film composite in PBS solution (pH 7.4, 37°C and 100 rpm) for fifteen weeks. Error bars refer to mean standard deviation of triplicate experimental data.

Figure 4

Fractional cumulative release of BP from PLA thin film composite in TrisHCl buffer solution, pH 7.4, at 37°C and 100 rpm for 11 weeks. Error bars refer to mean standard deviation of replicate experimental data.

Figure 5

Illustration of release stages for GM without and with HAp.

Figure 6

Illustration of the geometry.

Figure 7

The time dependence of diffusion coefficients for GM in PLA.

Figure 8

Drug release predicted (blue curve) for GM in PLA in comparison with measurement data (red dots).

Figure 9

Diffusion coefficients (Left) and drug release predicted (Right, blue curve) for BP in PLA in comparison with measurement data (red dots).

Figure 10

Predicted fractional release based on constant diffusion coefficients for GM (Left) and BP (Right).

Figure 11

Predicted fractional release based on effective diffusion coefficients (Temkin model) for GM (Left) and BP (Right).

Figure 12

Predicted fractional release based on the Robin boundary condition (8) for GM (Left) and BP (Right).