From Louvain to Leiden: guaranteeing well-connected communities

Abstract

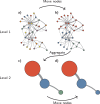
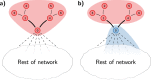
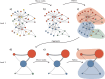
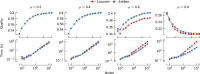
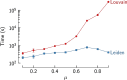
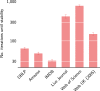
Community detection is often used to understand the structure of large and complex networks. One of the most popular algorithms for uncovering community structure is the so-called Louvain algorithm. We show that this algorithm has a major defect that largely went unnoticed until now: the Louvain algorithm may yield arbitrarily badly connected communities. In the worst case, communities may even be disconnected, especially when running the algorithm iteratively. In our experimental analysis, we observe that up to 25% of the communities are badly connected and up to 16% are disconnected. To address this problem, we introduce the Leiden algorithm. We prove that the Leiden algorithm yields communities that are guaranteed to be connected. In addition, we prove that, when the Leiden algorithm is applied iteratively, it converges to a partition in which all subsets of all communities are locally optimally assigned. Furthermore, by relying on a fast local move approach, the Leiden algorithm runs faster than the Louvain algorithm. We demonstrate the performance of the Leiden algorithm for several benchmark and real-world networks. We find that the Leiden algorithm is faster than the Louvain algorithm and uncovers better partitions, in addition to providing explicit guarantees.

Figure 1

Louvain algorithm. The Louvain algorithm starts from a singleton partition in which each node is in its own community (a). The algorithm moves individual nodes from one community to another to find a partition (b). Based on this partition, an aggregate network is created (c). The algorithm then moves individual nodes in the aggregate network (d). These steps are repeated until the quality cannot be increased further.

Figure 2

Disconnected community. Consider the partition shown in (a). When node 0 is moved to a different community, the red community becomes internally disconnected, as shown in (b). However, nodes 1–6 are still locally optimally assigned, and therefore these nodes will stay in the red community.

Figure 3

Leiden algorithm. The Leiden algorithm starts from a singleton partition (a). The algorithm moves individual nodes from one community to another to find a partition (b), which is then refined (c). An aggregate network (d) is created based on the refined partition, using the non-refined partition to create an initial partition for the aggregate network. For example, the red community in (b) is refined into two subcommunities in (c), which after aggregation become two separate nodes in (d), both belonging to the same community. The algorithm then moves individual nodes in the aggregate network (e). In this case, refinement does not change the partition (f). These steps are repeated until no further improvements can be made.

Figure 4

Badly connected communities. Percentage of communities found by the Louvain algorithm that are either disconnected or badly connected compared to percentage of badly connected communities found by the Leiden algorithm. Note that communities found by the Leiden algorithm are guaranteed to be connected.

Figure 5

Scaling of benchmark results for network size. Speed and quality of the Louvain and the Leiden algorithm for benchmark networks of increasing size (two iterations). For larger networks and higher values of μ, Louvain is much slower than Leiden. For higher values of μ, Leiden finds better partitions than Louvain.

Figure 6

Runtime versus quality for benchmark networks. Speed and quality for the first 10 iterations of the Louvain and the Leiden algorithm for benchmark networks (n = 10⁶ and n = 10⁷). The horizontal axis indicates the cumulative time taken to obtain the quality indicated on the vertical axis. Each point corresponds to a certain iteration of an algorithm, with results averaged over 10 experiments. In general, Leiden is both faster than Louvain and finds better partitions.

Figure 7

Scaling of benchmark results for difficulty of the partition. Speed of the first iteration of the Louvain and the Leiden algorithm for benchmark networks with increasingly difficult partitions (n = 10⁷). In the most difficult case (μ = 0.9), Louvain requires almost 2.5 days, while Leiden needs fewer than 10 minutes.

Figure 8

First iteration runtime for empirical networks. Speed of the first iteration of the Louvain and the Leiden algorithm for six empirical networks. Leiden is faster than Louvain especially for larger networks.

Figure 9

Runtime versus quality for empirical networks. Speed and quality for the first 10 iterations of the Louvain and the Leiden algorithm for six empirical networks. The horizontal axis indicates the cumulative time taken to obtain the quality indicated on the vertical axis. Each point corresponds to a certain iteration of an algorithm, with results averaged over 10 experiments. Leiden is both faster than Louvain and finds better partitions.

Figure 10

Number of iterations until stability. Number of iterations before the Leiden algorithm has reached a stable iteration for six empirical networks. In a stable iteration, the partition is guaranteed to be node optimal and subpartition γ-dense.