Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems

Abstract

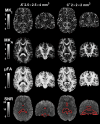
Microstructure imaging techniques based on tensor-valued diffusion encoding have gained popularity within the MRI research community. Unlike conventional diffusion encoding-applied along a single direction in each shot-tensor-valued encoding employs diffusion encoding along multiple directions within a single preparation of the signal. The benefit is that such encoding may probe tissue features that are not accessible by conventional encoding. For example, diffusional variance decomposition (DIVIDE) takes advantage of tensor-valued encoding to probe microscopic diffusion anisotropy independent of orientation coherence. The drawback is that tensor-valued encoding generally requires gradient waveforms that are more demanding on hardware; it has therefore been used primarily in MRI systems with relatively high performance. The purpose of this work was to explore tensor-valued diffusion encoding on clinical MRI systems with varying performance to test its technical feasibility within the context of DIVIDE. We performed whole-brain imaging with linear and spherical b-tensor encoding at field strengths between 1.5 and 7 T, and at maximal gradient amplitudes between 45 and 80 mT/m. Asymmetric gradient waveforms were optimized numerically to yield b-values up to 2 ms/μm2. Technical feasibility was assessed in terms of the repeatability, SNR, and quality of DIVIDE parameter maps. Variable system performance resulted in echo times between 83 to 115 ms and total acquisition times of 6 to 9 minutes when using 80 signal samples and resolution 2×2×4 mm3. As expected, the repeatability, signal-to-noise ratio and parameter map quality depended on hardware performance. We conclude that tensor-valued encoding is feasible for a wide range of MRI systems-even at 1.5 T with maximal gradient waveform amplitudes of 33 mT/m-and baseline experimental design and quality parameters for all included configurations. This demonstrates that tissue features, beyond those accessible by conventional diffusion encoding, can be explored on a wide range of MRI systems.

Fig 1

Schematic spin-echo sequence with echo planar imaging readout and diffusion-encoding gradient waveforms that yield linear (red line) and spherical b-tensor encoding (black lines). Note that the STE waveform is asymmetric around the refocusing pulse [20] and that it must therefore be designed to compensate for errors caused by concomitant fields [40]. The LTE waveform is bipolar to match the effective diffusion times for STE and LTE [41]. Note that crusher gradients (dotted lines) are not engaged when the diffusion encoding acts as a crusher.

Fig 2

DIVIDE parameter maps in transversal and coronal slices for configurations A-D. The image quality generally improves with higher field strength and gradient amplitude. Most notably there is a discernably higher level of noise for configuration A. Configuration D generally exhibited higher MK_A, a pronounced geometrical distortion at the anterior part of the brain, and more pronounced ghosting artifacts, as compared with the other configurations. Furthermore, large regions of negative MK_I were observed only for configuration D.

Fig 3

SNR maps at b = 2 ms/μm² in three transversal slices for configurations A-D and SNR distributions in the brain parenchyma at b = 0.1 and 2 ms/μm² (histograms). White outlines show the outer perimeter within which SNR > 3, and the red outlines show regions where SNR < 3. At high b-values, images from all systems exhibited low SNR in the ventricles due to the high diffusivity of CSF. Configuration A shows low SNR in the central and inferior parts of the brain. Configuration C exhibited the highest SNR across all b-values, but also a posterior rim of low SNR caused by poor fat suppression (red arrows). Configuration D generally exhibited high SNR in the peripheral regions; in the lower parts of the brain, it exhibited a heterogeneous SNR. It also exhibited an irregular perimeter in the inferior part of the brain, which was likely caused by local field heterogeneity in proximity to the ear canal and poor RF homogeneity, both commonly associated to dMRI at ultra-high field strengths [58].

Fig 4. Simulation of DIVIDE parameter accuracy and precision in three model tissues.

Markers show the mean parameter value, and the whiskers show one standard deviation across 10⁴ independent realizations of noise. The dashed horizontal lines show the parameter values that are estimated for a noise-free signal; deviation from the line indicates parameter bias caused by noise. As expected, precision and accuracy both improve with increasing SNR. The estimation of MD and μFA appear to be the most accurate and precise, although the μFA shows a deterioration of accuracy and precision when its true value is low (panel II) [19]. Both MK_A and MK_I suffer a positive bias when SNR in the b = 0 image is approximately 20 or less. Interestingly, MK_A is always more precise and accurate than MK_I, indicating that it is generally less sensitive to noise. The simulations show that signal noise can cause negative values for both MK_I and MK_A, which is especially likely when the true values are close to zero. Finally, in the case where MK_I = 0 (panel III), signal noise did not cause a strong positive bias in MK_I for SNR levels that match configuration C (where the majority of voxels have SNR > 20 at b = 0.1 ms/μm², Fig 3). This suggests that signal noise alone is not likely to explain the positive MK_I that is observed throughout the brain parenchyma.

Fig 5

DIVIDE parameters and SNR maps for configurations A* and C*. The parameter maps from configuration A* are markedly less noisy than at the original resolution shown in Fig 2. For configuration C*, the resolution was increased, while maintaining high SNR in the superior and peripheral parts of the brain, although inferior and central parts showed regions where SNR was below 3 and may therefore suffer from non-negligible signal bias.

Fig 6

Parameter maps from repeated acquisitions and analysis of repeatability for configurations A-D. The voxel-wise difference (Diff.) between the first and second acquisition (Acq. 1 and 2) is color coded in red-green. The normalized powder-averaged signal at b = 2 ms/μm² (A(L) and A(S)) is given in percent, and the MD is given in units of μm²/ms. The difference maps show the largest differences in tissue interfaces where small misregistration between the first and second acquisition causes large parameter discrepancy. Bland-Altman plots show the distributions of voxel-wise differences in tissue where μFA < 0.7 and MD < 1.5 μm²/ms. Solid and dashed lines show the average and two standard deviations of the distributions. All configurations showed negligible bias in repeatability of signal and DIVIDE parameters, and a configuration-dependent parameter precision. Note that the estimated precision pertains to the per-voxel parameter uncertainty; analyzing the average over multiple voxels is expected to markedly improve the precision.