Bayes-optimal estimation of overlap between populations of fixed size
- PMID: 30925165
- PMCID: PMC6440621
- DOI: 10.1371/journal.pcbi.1006898
Bayes-optimal estimation of overlap between populations of fixed size
Abstract
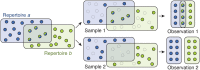
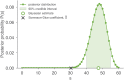
Measuring the overlap between two populations is, in principle, straightforward. Upon fully sampling both populations, the number of shared objects-species, taxonomical units, or gene variants, depending on the context-can be directly counted. In practice, however, only a fraction of each population's objects are likely to be sampled due to stochastic data collection or sequencing techniques. Although methods exists for quantifying population overlap under subsampled conditions, their bias is well documented and the uncertainty of their estimates cannot be quantified. Here we derive and validate a method to rigorously estimate the population overlap from incomplete samples when the total number of objects, species, or genes in each population is known, a special case of the more general β-diversity problem that is particularly relevant in the ecology and genomic epidemiology of malaria. By solving a Bayesian inference problem, this method takes into account the rates of subsampling and produces unbiased and Bayes-optimal estimates of overlap. In addition, it provides a natural framework for computing the uncertainty of its estimates, and can be used prospectively in study planning by quantifying the tradeoff between sampling effort and uncertainty.
Conflict of interest statement
The author has declared that no competing interests exist.
Figures

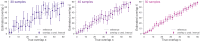
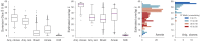

References
-
- Whittaker RH. Vegetation of the Siskiyou mountains, Oregon and California. Ecological Monographs. 1960;30(3):279–338. 10.2307/1943563 - DOI
-
- Koleff P, Gaston KJ, Lennon JJ. Measuring beta diversity for presence–absence data. Journal of Animal Ecology. 2003;72(3):367–382. 10.1046/j.1365-2656.2003.00710.x - DOI
-
- Rao CR. Diversity and dissimilarity coefficients: a unified approach. Theoretical Population Biology. 1982;21(1):24–43. 10.1016/0040-5809(82)90004-1 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

