A novel, FFT-based one-dimensional blood flow solution method for arterial network

Abstract

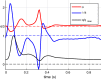
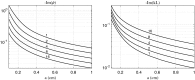
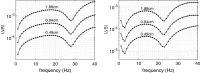
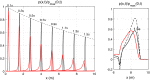
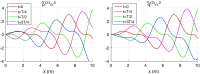
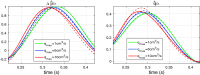
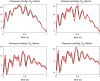
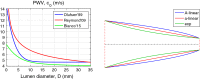
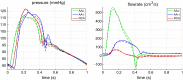
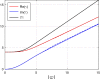
In the present work, we propose an FFT-based method for solving blood flow equations in an arterial network with variable properties and geometrical changes. An essential advantage of this approach is in correctly accounting for the vessel skin friction through the use of Womersley solution. To incorporate nonlinear effects, a novel approximation method is proposed to enable calculation of nonlinear corrections. Unlike similar methods available in the literature, the set of algebraic equations required for every harmonic is constructed automatically. The result is a generalized, robust and fast method to accurately capture the increasing pulse wave velocity downstream as well as steepening of the pulse front. The proposed method is shown to be appropriate for incorporating correct convection and diffusion coefficients. We show that the proposed method is fast and accurate and it can be an effective tool for 1D modelling of blood flow in human arterial networks.

Keywords: 1D arterial haemodynamics; Fast Fourier transform (FFT); Perturbation method; Pulse wave propagation.

Fig. 1

Variation of the nonlinearity coefficient $\alpha$ (red) and the friction coefficient $\gamma$ (divided by 4) (blue) over a cardiac cycle. Normalized flow rate waveform is shown in black. These results are computed using the 3D modelling of the flow in a Carotid artery described in Sazonov et al. (2011)

Fig. 2

Dependence of the imaginary part of the $\varphi$ parameter (left) and the total phase incursion kL (right) on lumen radius a and frequency f (indicated above every curve in Hz). Here $L=10\text{cm}$ is taken

Fig. 3

Accuracy of the reflection coefficient $\Delta R=|R_{\mathrm{numer}}-R_{\mathrm{conic}}|$ (left) and transmission coefficient $\Delta S=|S_{\mathrm{numer}}-S_{\mathrm{conic}}|$ versus frequency f for different element lengths h (indicated above every curve)

Fig. 4

Left: propagation of a Gaussian-shape pulse along a 10 m pipe of the 2 cm diameter with $c_0=6.17\text{m/s}$. Black: $\gamma =11$; Red: Womersley’s profile-based decay. Dashed line indicates the theoretical decay (93). Right: propagation of a realistic waveform along the same pipe at $t=1.5\text{s}$ for $\gamma =11$ (black solid), for $\gamma =4$ (black dashed), and for Womersley’s profile-based decay (red)

Fig. 5

Dimensionless nonlinear corrections for the pressure ${\widehat{p}}^{(2)}/{\epsilon }^2$ (left) and the flowrate ${\widehat{q}}^{(2)}/{\epsilon }^2$ (right) for the waveform, (95), with $\xi =0.5$. Solid lines: the exact solution, (96) and (97); dashed darker lines: results of the numerical calculations, (84) with $h=2\text{cm}$

Fig. 6

Pressure (left) and flow rate (right) waveforms computed at the inlet, 1, midpoint, 2, outlet, 3, of the first pipe and outlet of the conic segment, 4. The pressure waveform in cite 4 not presented as it is almost identical to that of at site 3. Coloured curves are computed using the method described in Carson and Van Loon (2017), dashed black curves are computed using the proposed method

Fig. 7

Part of the normalized pressure (left) and flow rate (right) waveforms computed at site 3 (inlet of the tapering segment) in the vicinity of the main peak for different peak flow rate values (indicated in the legend). The solid coloured lines are computed using the method in Carson and Van Loon (2017), and the dashed lines are computed using the proposed method

Fig. 8

Normalized nonlinear corrections for the pressure (left) and flow rate (right) waveforms computed at site 3 for different flow rate peak values of the inlet flow. The colours are the same as in Fig. 7. Normalized waveforms ${\widehat{p}}^{(2)}/{\epsilon }^2$ and ${\widehat{q}}^{(2)}/{\epsilon }^2$ computed using the proposed method is independent of the amplitude and indicated by black dashed curve

Fig. 9

Comparison of measured (black) and computed (red) pressure waveforms. The experimental setup is described in Sazonov et al. (2017)

Fig. 10

Left: The $c_0$ vs lumen diameter D approximations. Blue: Olufsen (1999), Mynard et al. (2010), Mynard and Smolich (2015); Red: Reymond et al. (2009); Green: Blanco et al. (2015). Right: Different types of vessel shape approximation. Blue: A(x) is linear. Red: a(x) is linear. Green: A, a are exponential

Fig. 11

Arterial network model described in Mynard and Smolich (2015) and used here for simulation: main arteries (a), cerebral arteries (b), coronary arteries (c)

Fig. 12

Pressure wave form (left) and flow rate waveform (right). Computed waveforms at the beginning of aortic arc (green), at the beginning of abdominal aorta (blue) and at the midpoint of the right carotid (red). Waveforms computed by the model in Mynard and Nithiarasu (2008) are shown using solid lines and those computed by the proposed method are shown by dashed lines

Fig. 13

Dependence of real part (red), imaginary part (blue) and absolute value (black) of the $\gamma$ parameter on the Womersley number $|\varpi |=a_0\sqrt{\omega /2\nu }$. Dashed lines indicate an approximation (131)