Estimation in emerging epidemics: biases and remedies
- PMID: 30958162
- PMCID: PMC6364646
- DOI: 10.1098/rsif.2018.0670
Estimation in emerging epidemics: biases and remedies
Abstract
When analysing new emerging infectious disease outbreaks, one typically has observational data over a limited period of time and several parameters to estimate, such as growth rate, the basic reproduction number R0, the case fatality rate and distributions of serial intervals, generation times, latency and incubation times and times between onset of symptoms, notification, death and recovery/discharge. These parameters form the basis for predicting a future outbreak, planning preventive measures and monitoring the progress of the disease outbreak. We study inference problems during the emerging phase of an outbreak, and point out potential sources of bias, with emphasis on: contact tracing backwards in time, replacing generation times by serial intervals, multiple potential infectors and censoring effects amplified by exponential growth. These biases directly affect the estimation of, for example, the generation time distribution and the case fatality rate, but can then propagate to other estimates such as R0 and growth rate. We propose methods to remove or at least reduce bias using statistical modelling. We illustrate the theory by numerical examples and simulations.
Keywords: basic reproduction number; emerging epidemic; estimation bias; statistics.
Conflict of interest statement
We declare we have no competing interests.
Figures
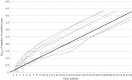
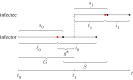
References
-
- Diekmann O, Heesterbeek H, Britton T. 2013. Mathematical tools for understanding infectious disease dynamics. Princeton, NJ: Princeton University Press.
-
- Anderson RM, May RM. 1991. Infectious diseases of humans: dynamics and control. New York, NY: Wiley.
-
- Kermack WO, McKendrick AG. 1927. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721. Reprinted as Bull. Math. Bio. (1991). 53, 33–55 (10.1098/rspa.1927.0118) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
