Deformation-Induced Phase Transitions in iPP Polymorphs
- PMID: 30965850
- PMCID: PMC6418605
- DOI: 10.3390/polym9100547
Deformation-Induced Phase Transitions in iPP Polymorphs
Abstract
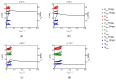
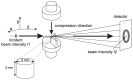
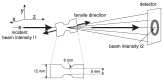
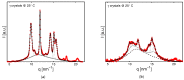
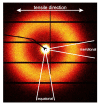
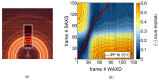
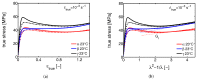
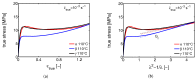
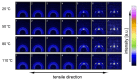
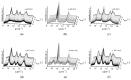
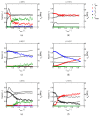
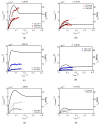
This detailed study reveals the relation between structural evolution and the mechanical response of α -, β - and γ -iPP. Uni-axial compression experiments, combined with in situ WAXD measurements, allowed for the identification of the evolution phenomena in terms of phase composition. Tensile experiments in combination with SAXS revealed orientation and voiding phenomena, as well as structural evolution in the thickness of the lamellae and amorphous layers. On the level of the crystallographic unit cell, the WAXD experiments provided insight into the early stages of deformation. Moreover, transitions in the crystal phases taking place in the larger deformation range and the orientation of crystal planes were monitored. At all stretching temperatures, the crystallinity decreases upon deformation, and depending on the temperature, different new structures are formed. Stretching at low temperatures leads to crystal destruction and the formation of the oriented mesophase, independent of the initial polymorph. At high temperatures, above T α c , all polymorphs transform into oriented α -iPP. Small quantities of the initial structures remain present in the material. The compression experiments, where localization phenomena are excluded, show that these transformations take place at similar strains for all polymorphs. For the post yield response, the strain hardening modulus is decisive for the mechanical behavior, as well as for the orientation of lamellae and the evolution of void fraction and dimensions. β -iPP shows by far the most intense voiding in the entire experimental temperature range. The macroscopic localization behavior and strain at which the transition from disk-like void shapes, oriented with the normal in tensile direction, into fibrillar structures takes place is directly correlated with the strain hardening modulus.
Keywords: cavitation; deformation; in situ X-ray; isotactic polypropylene; phase transitions; polymorphism; temperature; uniaxial compression; uniaxial tensile deformation.
Conflict of interest statement
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Figures












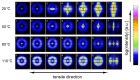


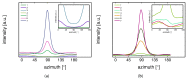

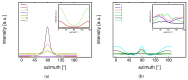



References
-
- Brückner S., Meille S., Petraccone V., Pirozzi B. Polymorphism in isotactic polypropylene. Prog. Polym. Sci. 1991;16:361–404. doi: 10.1016/0079-6700(91)90023-E. - DOI
-
- Lotz B., Wittmann J., Lovinger A. Structure and morphology of poly(propylenes): A molecular analysis. Polymer. 1996;37:4979–4992. doi: 10.1016/0032-3861(96)00370-9. - DOI
-
- De Rosa C., Auriemma F., Di Capua A., Resconi L., Guidotti S., Camurati I., Nifant’ev I., Laishevtsev I. Structure-property correlations in polypropylene from metallocene catalysts: Stereodefective, regioregular isotactic polypropylene. J. Am. Chem. Soc. 2004;126:17040–17049. doi: 10.1021/ja045684f. - DOI - PubMed
-
- Varga J. β-modification of isotactic polypropylene: Preparation, structure, processing, properties, and application. J. Macromol. Sci. Phys. 2002;41:1121–1171. doi: 10.1081/MB-120013089. - DOI
-
- Roozemond P., Van Erp T., Peters G. Flow-induced crystallization of isotactic polypropylene: Modeling formation of multiple crystal phases and morphologies. Polymer. 2016;89:69–80. doi: 10.1016/j.polymer.2016.01.032. - DOI
LinkOut - more resources
Full Text Sources

