Statistical physics of liquid brains
- PMID: 31006368
- PMCID: PMC6553585
- DOI: 10.1098/rstb.2018.0376
Statistical physics of liquid brains
Abstract
Liquid neural networks (or 'liquid brains') are a widespread class of cognitive living networks characterized by a common feature: the agents (ants or immune cells, for example) move in space. Thus, no fixed, long-term agent-agent connections are maintained, in contrast with standard neural systems. How is this class of systems capable of displaying cognitive abilities, from learning to decision-making? In this paper, the collective dynamics, memory and learning properties of liquid brains is explored under the perspective of statistical physics. Using a comparative approach, we review the generic properties of three large classes of systems, namely: standard neural networks (solid brains), ant colonies and the immune system. It is shown that, despite their intrinsic physical differences, these systems share key properties with standard neural systems in terms of formal descriptions, but strongly depart in other ways. On one hand, the attractors found in liquid brains are not always based on connection weights but instead on population abundances. However, some liquid systems use fluctuations in ways similar to those found in cortical networks, suggesting a relevant role for criticality as a way of rapidly reacting to external signals. This article is part of the theme issue 'Liquid brains, solid brains: How distributed cognitive architectures process information'.
Keywords: brains; collective intelligence; criticality; evolution; phase transitions.
Conflict of interest statement
We have no competing interests.
Figures



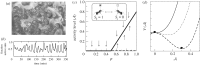



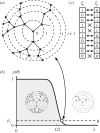
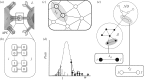

References
-
- Hopfield JJ. 1994. Physics, computation and why biology looks so different. J. Theor. Biol. 171, 53–60. (10.1006/jtbi.1994.1211) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
