The distribution of epistasis on simple fitness landscapes

Abstract

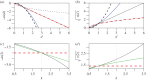
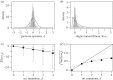
Fitness interactions between mutations can influence a population's evolution in many different ways. While epistatic effects are difficult to measure precisely, important information is captured by the mean and variance of log fitnesses for individuals carrying different numbers of mutations. We derive predictions for these quantities from a class of simple fitness landscapes, based on models of optimizing selection on quantitative traits. We also explore extensions to the models, including modular pleiotropy, variable effect sizes, mutational bias and maladaptation of the wild type. We illustrate our approach by reanalysing a large dataset of mutant effects in a yeast snoRNA (small nucleolar RNA). Though characterized by some large epistatic effects, these data give a good overall fit to the non-epistatic null model, suggesting that epistasis might have limited influence on the evolutionary dynamics in this system. We also show how the amount of epistasis depends on both the underlying fitness landscape and the distribution of mutations, and so is expected to vary in consistent ways between new mutations, standing variation and fixed mutations.

Keywords: Fisher’s geometric model; Saccharomyces cerevisiae; fitness landscapes; genetic interactions.

Figure 1.

Predictions for mean log fitness (a,c) or the standard deviation in log fitness (b,d). (a,b) show predictions for individuals carrying different numbers of mutations, d. (c,d) shows results for double mutants (d = 2), varying the curvature of the fitness landscape, k. Results for the null model, with no epistasis, are shown as red dashed lines. In this case, the mean and variance in log fitness both change linearly with d (equations (3) and (4)). Results for simple phenotypic models are shown as black lines. The upper panels show results with no epistasis on average (solid lines, k = 2), negative epistasis on average (dashed lines, k = 4) or positive epistasis on average (dotted lines, k = 1). Blue lines show results for a model with strongly biased mutations (β = 3, k = 2; electronic supplementary material, equations (48) and (50)). Green lines show results where the mutations on each trait are drawn from a leptokurtic reflected exponential distribution (electronic supplementary material, equation (43)). (Online version in colour.)

Figure 2.

Reanalysis of mutations in Saccharomyces cerevisiae U3 snoRNA (small nucleolar RNA) [1]. (a) Distribution of pairwise epistatic effects (equation (5)), compared with the predictions of the simplest phenotypic model with k = 2: ɛ ∼ N(0, 2Var(ln w₁)) (black line; [32]; electronic supplementary material, appendix A), and a normal distribution with matching mean and variance (dotted line). (b) Distribution of single-mutant log fitnesses, and the best-fit shifted gamma distribution, as predicted by the simplest phenotypic models [29]. (c) Mean of the log fitnesses of individuals carrying d mutations (black points with barely visible standard error bars); the median and 90% quantiles (grey points and bars); the analytical prediction, which applies to both the null model and the phenotypic model with k = 2 (solid line; equations (3) and (8)); and the best-fit regression for ln m(d) ∼ ln d (dotted line, which has a slope implying $\hat{k}=2.16$). (d) Standard deviation in the log fitnesses of individuals carrying d mutations (black points with barely visible standard error bars); analytical predictions from the null model, equation (4) (dashed line), or the phenotypic model with k = 2, equation (9) (solid line); and the best-fit regression of ln v(d) ∼ ln d (dotted line, which has slope 0.89).