Invasion reproductive numbers for discrete-time models

Abstract

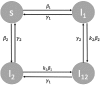
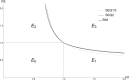
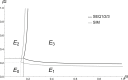
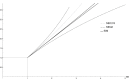
Although invasion reproductive numbers (IRNs) are utilized frequently in continuous-time models with multiple interacting pathogens, they are yet to be explored in discrete-time systems. Here, we extend the concept of IRNs to discrete-time models by showing how to calculate them for a set of two-pathogen SIS models with coinfection. In our exploration, we address how sequencing events impacts the basic reproductive number (BRN) and IRN. As an illustrative example, our models are applied to rhinovirus and respiratory syncytial virus co-circulation. Results show that while the BRN is unaffected by variations in the order of events, the IRN differs. Furthermore, our models predict copersistence of multiple pathogen strains under cross-immunity, which is atypical of analogous continuous-time models. This investigation shows that sequencing events has important consequences for the IRN and can drastically alter competition dynamics.

Keywords: Coinfection; Competitive exclusion; Discrete-time model; Invasion reproductive number.

Fig. 1

SIS coinfection model for two pathogens.

Fig. 2

BRN/IRN Threshold Curves$k_i>1$. In this graph, $g_1=g_2=0.4$ and $k_1=k_2=2$. In region $E_0$, we see extinction of both pathogens, in $E_1$, the persistence of only pathogen 1, in $E_2$, the persistence of only pathogen 2, and in $E_3$, co-persistence of both pathogens.

Fig. 3

BRN/IRN Threshold Curves for$k_i<1$. In this graph, $g_1=g_2=0.4$ and $k_1=k_2=0.7$. In region $E_0$, we see extinction of both pathogens, in $E_1$, the persistence of only pathogen 1, in $E_2$, the persistence of only pathogen 2, and in $E_3$, co-persistence of both pathogens.

Fig. 4

BRN/IRN Threshold Curves${\beta }_1$vs.${\beta }_2$. In this graph, $g_1=0.15$, $g_2=0.24$, $k_1=0.7$ and $k_2=1.5$. In region $E_0$, we see extinction of both pathogens, in $E_1$, the persistence of only pathogen 1, in $E_2$, the persistence of only pathogen 2, and in $E_3$, co-persistence of both pathogens. The dotted gray box delineates the $E_0$ region for the SIM model while the dotted black box delineates the $E_0$ region for the SEQ1, SEQ2, and SEQ3 models.

Fig. 5

Coexistence with Complete Cross-Immunity. The parameter values used to generate this figure are $g_1=0.15,g_2=0.24,k_1=k_2=0$. With these parameter values, we witness the possibility of coexistence of the two pathogen strains in the SEQ and SIM models.