Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Apr 26;19(9):1966.
doi: 10.3390/s19091966.

A Lagrange-Newton Method for EIT/UT Dual-Modality Image Reconstruction

Guanghui Liang  1 , Shangjie Ren  2 , Shu Zhao  3 , Feng Dong  4
Affiliations

A Lagrange-Newton Method for EIT/UT Dual-Modality Image Reconstruction

Guanghui Liang et al. Sensors (Basel). .

Abstract

An image reconstruction method is proposed based on Lagrange-Newton method for electrical impedance tomography (EIT) and ultrasound tomography (UT) dual-modality imaging. Since the change in conductivity distribution is usually accompanied with the change in acoustic impedance distribution, the reconstruction targets of EIT and UT are unified to the conductivity difference using the same mesh model. Some background medium distribution information obtained from ultrasound transmission and reflection measurements can be used to construct a hard constraint about the conductivity difference distribution. Then, the EIT/UT dual-modality inverse problem is constructed by an equality constraint equation, and the Lagrange multiplier method combining Newton-Raphson iteration is used to solve the EIT/UT dual-modality inverse problem. The numerical and experimental results show that the proposed dual-modality image reconstruction method has a better performance than the single-modality EIT method and is more robust to the measurement noise.

Keywords: dual-modality imaging; electrical impedance tomography; lagrange-newton method; ultrasound tomography.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest.

Figures

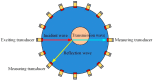
Figure 1
Figure 1
Ultrasound transmission and reflection physical model.
Figure 2
Figure 2
3-D sensitivity distribution: (a) Electrical impedance tomography (EIT), (b) ultrasound tomography (UT).
Figure 3
Figure 3
Mesh model of EIT/UT dual-modality imaging.
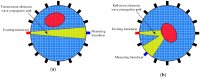
Figure 4
Figure 4
Schematic diagram of ultrasonic wave propagation path: (a) there is no target on the ultrasonic waves propagation path, (b) there is a target on the ultrasonic waves propagation path.
Figure 5
Figure 5
Reconstruction results with no noise.
Figure 6
Figure 6
Reconstruction results with 40 dB noise.
Figure 7
Figure 7
Reconstruction results with 25 dB noise.
Figure 8
Figure 8
Reconstruction results with 20 dB noise.
Figure 9
Figure 9
Mean value of the quantitative indexes.
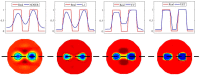
Figure 10
Figure 10
Contour of the reconstructed images along the center horizontal line.
Figure 11
Figure 11
EIT/UT dual-modality data acquisition system.
Figure 12
Figure 12
Reconstruction results of the experimental tests.
Figure 13
Figure 13
Quantitative analysis of the experimental results.
See this image and copyright information in PMC

References

    1. Dong F., Jiang Z.X., Qiao X.T., Xu L.A. Application of electrical resistance tomography to two-phase pipe flow parameters measurement. Flow Meas. Instrum. 2003;14:183–192. doi: 10.1016/S0955-5986(03)00024-4. - DOI
    1. Yao J.F., Takei M. Application of process tomography to multiphase flow measurement in industrial and biomedical fields—A review. IEEE Sens. J. 2017;17:8196–8205. doi: 10.1109/JSEN.2017.2682929. - DOI
    1. Liu D., Khambampati A.K., Du J.F. A parametric level set method for electrical impedance tomography. IEEE Trans. Med. Imaging. 2018;37:451–460. doi: 10.1109/TMI.2017.2756078. - DOI - PubMed
    1. Nissinen A., Kaipio J.P., Vauhkonen M., Kolehmainen V. Contrast enhancement in EIT imaging of the brain. Physiol. Meas. 2015;37:1–24. doi: 10.1088/0967-3334/37/1/1. - DOI - PubMed
    1. Storz H., Storz W., Jacobs F. Electrical resistivity tomography to investigate geological structures of the earth’s upper crust. Geophys. Prospect. 2000;48:455–471. doi: 10.1046/j.1365-2478.2000.00196.x. - DOI

LinkOut - more resources