Bridging the Homogeneous-Heterogeneous Divide: Modeling Spin for Reactivity in Single Atom Catalysis

Abstract

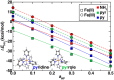
Single atom catalysts (SACs) are emergent catalytic materials that have the promise of merging the scalability of heterogeneous catalysts with the high activity and atom economy of homogeneous catalysts. Computational, first-principles modeling can provide essential insight into SAC mechanism and active site configuration, where the sub-nm-scale environment can challenge even the highest-resolution experimental spectroscopic techniques. Nevertheless, the very properties that make SACs attractive in catalysis, such as localized d electrons of the isolated transition metal center, make them challenging to study with conventional computational modeling using density functional theory (DFT). For example, Fe/N-doped graphitic SACs have exhibited spin-state dependent reactivity that remains poorly understood. However, spin-state ordering in DFT is very sensitive to the nature of the functional approximation chosen. In this work, we develop accurate benchmarks from correlated wavefunction theory (WFT) for relevant octahedral complexes. We use those benchmarks to evaluate optimal DFT functional choice for predicting spin state ordering in small octahedral complexes as well as models of pyridinic and pyrrolic nitrogen environments expected in larger SACs. Using these guidelines, we determine Fe/N-doped graphene SAC model properties and reactivity as well as their sensitivities to DFT functional choice. Finally, we conclude with broad recommendations for computational modeling of open-shell transition metal single-atom catalysts.

Keywords: catalysis; density functional theory; single atom catalysis; spin state crossover; transition metal chemistry.

Figure 1

Iron catalysts in three classes: homogeneous tetraphenyl porphyrin (Top), N-doped graphene single atom catalysts (SACs, Middle), and heterogeneous hematite (Bottom). In all cases, carbon is shown in gray, nitrogen in blue, iron in purple, and oxygen in red.

Figure 2

CASPT2 spin splitting energetics in kcal/mol for ΔE_H−L (circles) and ΔE_H−I (triangles), as indicated in inset, of hexa-aqua (top) and hexa-ammine (bottom) transition metal complexes. Results are shown for 3 IPEA shifts: 0.00 (blue symbols), 0.50 (dark gray symbols), and 1.50 (red symbols) a.u.. Both M(II) and M(III) complexes are shown sorted by the number of 3d electrons, from Ti²⁺ to Cu³⁺.

Figure 3

Sensitivity of spin-state splitting with respect to HF exchange (i.e., ∂ΔE_H−L/∂a_HF, in kcal/mol^.HFX) for hexa-aqua (top) and hexa-ammine (bottom) transition metal complexes. Both M(II) and M(III) complexes are shown grouped by their nominal d filling from 3 to 7 3d electrons for V(II) to Ni(III). For the 4, 5, and 6 d-electron cases, the energy gap corresponds to high-spin/intermediate-spin rather than high-spin/low-spin. Shaded bars indicate that spin contamination could not be eliminated for both spin states and sensitivity may not be reliable.

Figure 4

(Left) Spin-splitting energetics (in kcal/mol) corresponding to ΔE_H−I for Cr²⁺-Co³⁺ and ΔE_H−L for all other cases shown for hexa-aqua (Top) and hexa-ammine (Bottom) complexes. Modified PBE0 GGA hybrid results are shown as circles. The exchange fraction, a_HF, is colored from blue for 0.0 (pure GGA) to red for 1.0 (full HF exchange), according to the inset legend. Reference CASPT2 results with the extended active space and IPEA shift of 0.5 a.u. are shown as green horizontal lines. The PBE0-DH results are shown as orange triangles. (Right) MAE (in kcal/mol) at several exchange fractions for the hexa-aqua and hexa-ammine complexes indicated at left.

Figure 5

Sensitivity to HF exchange fraction (a_HF) of high-spin/low-spin splitting (ΔE_H−L, in kcal/mol) for Fe(II) (squares) and Fe(III) (circles) homoleptic octahedral transition metal complexes with NH₃ (red symbols), pyridine (blue symbols), and pyrrole (green symbols) ligands. The structures of pyridine and pyrrole compounds are shown in inset in ball and stick (gray carbon, blue nitrogen, white hydrogen, and orange for iron). A zero axis is shown that indicates change in favored ground state spin.

Figure 6

Molecular structures (left) and singly occupied d_xz and d_z² spin-up molecular orbitals (right) for FeN₄C₁₀ and FeN₄C₁₂ graphene flake SAC models in the triplet state. The positive and negative phases of the wavefunction are shown in red and blue, respectively. An isosurface of 0.01 e/Bohr³ was used for the orbitals of FeN₄C₁₀ and of 0.03 e/Bohr³ for those of FeN₄C₁₂ for clarity. All structures are shown in ball and stick representation with carbon in brown, hydrogen in white, nitrogen in light blue, and iron in orange.

Figure 7

Spin-splitting energetics (in kcal/mol) for singlet-quintet (S-Q, red circles) or triplet-quintet (T-Q, blue circles) spin states vs. % HF exchange for pyridinic (FeN₄C₁₀, top) and pyrrolic (FeN₄C₁₂, bottom) SAC models. The 25% exchange in standard PBE0 is indicated as a vertical dashed line.

Figure 8

Reaction energetics (ΔE_rxn, in kcal/mol) for oxo formation from N₂O oxidant vs. % HF exchange for pyridinic (FeN₄C₁₀, top) and pyrrolic (FeN₄C₁₂, bottom) SAC models. The reaction is shown in inset. In each case, singlet (red circles), triplet (blue circles), and quintet (green circles) oxo formation energies are shown. The 25% exchange in standard PBE0 is indicated as a vertical dashed line.

Figure 9

Periodic structures for pyridinic and pyrrolic periodic SAC models in the triplet state with spin density shown. Positive spin density is shown in red and negative spin density is shown in blue, with an isosurface value of 0.03 e/Bohr³. All structures are shown in ball and stick representation with carbon in brown, nitrogen in light blue, and iron in orange.

Figure 10

The HSE06 projected density of states (PDOS) for spin up (Top) and down (Bottom, reflected curves) triplet pyridinic (Left) and pyrrolic (Right) SAC models. The 3d Fe orbital PDOS are shown as indicated in inset legends as solid curves except for yz and xz in the pyrrolic case, which are shown as dashed lines due to their degeneracy. The average PDOS for a 2p orbital from C (brown) or N (dark blue) are shown as translucent shaded regions. All energy levels (in eV) are aligned to the Fermi level (E_F), which is shown as a vertical dashed line. Some d levels have been truncated by the y-axis range to be able to compare to the broader C 2p and N 2p features.