Entropic Forces Drive Cellular Contact Guidance

Abstract

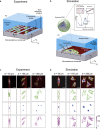
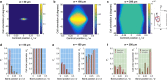
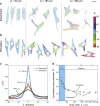
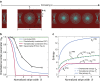
Contact guidance-the widely known phenomenon of cell alignment induced by anisotropic environmental features-is an essential step in the organization of adherent cells, but the mechanisms by which cells achieve this orientational ordering remain unclear. Here, we seeded myofibroblasts on substrates micropatterned with stripes of fibronectin and observed that contact guidance emerges at stripe widths much greater than the cell size. To understand the origins of this surprising observation, we combined morphometric analysis of cells and their subcellular components with a, to our knowledge, novel statistical framework for modeling nonthermal fluctuations of living cells. This modeling framework is shown to predict not only the trends but also the statistical variability of a wide range of biological observables, including cell (and nucleus) shapes, sizes, and orientations, as well as stress-fiber arrangements within the cells with remarkable fidelity with a single set of cell parameters. By comparing observations and theory, we identified two regimes of contact guidance: 1) guidance on stripe widths smaller than the cell size (w ≤ 160 μm), which is accompanied by biochemical changes within the cells, including increasing stress-fiber polarization and cell elongation; and 2) entropic guidance on larger stripe widths, which is governed by fluctuations in the cell morphology. Overall, our findings suggest an entropy-mediated mechanism for contact guidance associated with the tendency of cells to maximize their morphological entropy through shape fluctuations.

Figure 1

Experimental setup and representative images of the experimental data and simulations. (a) A sketch of the experimental setup of myofibroblasts seeded on a flat substrate micropatterned with FN (maroon) stripes of width w is shown. (Although each experimental substrate had one stripe width, for conciseness, the sketch shows different stripe widths on the same substrate.) (b) An illustration of the cell model employed in the simulations using homeostatic mechanics framework is given. The sketch shows a section of a cell on a FN stripe of width w and exchanging species with the nutrient bath. The inset shows a representative volume element of the cell cytoplasm containing polymerized actomyosin stress fibers and the unbound proteins, along with the energy landscape that governs the equilibrium of these proteins. (c) Immunofluorescence images of myofibroblasts on FN stripes of 50, 160, and 390 μm showing the actin cytoskeleton (green), nucleus (blue), and focal adhesions (magenta) are given; the edges of the stripes are indicated by dashed lines. (d) Corresponding predictions from the homeostatic mechanics framework with focal adhesions parametrized by the magnitude of the normalized traction $\hat{\text{T}}$ are shown (see Supporting Materials and Methods, Section S2.5.1). The scale bar in (c) and (d) represents 60 μm, and the width of the FN stripes is indicated by the maroon dashed lines for the two narrowest stripes. To see this figure in color, go online.

Figure 2

Experimental and computational data on key observables. Images of randomly selected (a) experimentally observed and (b) computationally predicted cell morphologies, showing their actin cytoskeleton and shaded to indicate the cell orientation ϕ, are given (definition of ϕ shown in the inset, with the best-fit ellipses and the corresponding major axis indicated on the cell images). The images are shown for cells on three selected widths of FN stripes with the scale bar in (a) and (b) representing 60 μm. (c) Measurements and predictions of the cell orientational order parameter Θ vs. stripe width w are shown. Box-and-whisker diagrams of experimental and computational data of the distributions of (d) cell orientation ϕ, (e) aspect ratio A_s, and (f) area A for the range of stripe widths investigated here are given. The boxes show the quartiles of the distributions, with the whiskers indicating the outliers in the experiments and the 5th and 95th percentiles of the distributions in the simulations. The mean of the distributions is depicted by semicircles for both measurements and simulations. In (c)–(f), the two regimes of contact guidance transitioning at a stripe width w ≈ 160 μm are indicated, and the experimental data set comprised at least 50 observations per stripe width. To see this figure in color, go online.

Figure 3

(a–c) Predictions of the joint probability density distributions p(x_c/w, ϕ) of the cell centroid being located at position x₁ = x_c within the stripe and having an orientation ϕ. Results are shown for three selected stripe widths w, with the inset defining x_c and ϕ. With decreasing w, the distributions become more heterogeneous, with cells unable to adopt an isotropic distribution of orientations, especially near the stripe edges. Note the differences in the color scales of the probability densities between the different subparts. (d–f) Measurements (from 50 observations per stripe width) and predictions of the probability P_x of the cell centroid location across the stripe (left) and the conditional order parameter Θ|_x of cells within each band centered at location x (right). In plots (d)–(f), each stripe is divided into bands of equal width, and the symmetric results shown for |x|, varying from the stripe center (x = 0) to the stripe edge at |x|/w = 0.5. To see this figure in color, go online.

Figure 4

Experimental and computational data for the stress-fiber distributions. (a) Experiments and (b) simulations of the stress-fiber distributions within cells on three stripe widths w are shown. The region with no stress fibers is the passive nucleus in the 2D model. The stress fibers are colored by their orientation as parametrized by the measure $\overline{\phi }$ that is invariant to rigid-body rotations of the cell. The scale bar in (a) and (b) represents 60 μm. (c) The corresponding predictions and measurements of the probability density functions $p\left(\overline{\phi }\right)$ over the ensemble of cell morphologies for three selected stripe widths are shown. (d) Predictions and measurements of the cytoskeletal order parameter $\mathcal{R}$ extracted from $p\left(\overline{\phi }\right)$ as a function of w are shown. The experimental data set in (c) and (d) comprised 50 observations, with both the experiments and simulations illustrating that cytoskeletal changes, as parametrized via stress-fiber polarization, only commence in regime II. To see this figure in color, go online.

Figure 5

Homeostatic temperature, traction forces, and guidance forces. (a) Predictions of the variation of the normalized homeostatic temperature $1/\hat{\zeta }$ and average normalized total traction force $\langle {\hat{\text{T}}}_{\text{T}}\rangle$ with stripe width w. Predictions of the spatial distributions of normalized tractions $\hat{\text{T}}$ are also included for randomly selected cell morphologies on three stripe widths (outline of nucleus shown as a black line) with the scale bars, 60 μm. Both homeostatic temperature and total traction forces only change with stripe width in regime II; see Supporting Materials and Methods, Section S2.5 for a more detailed discussion on the traction predictions. (b) Predictions of the total guidance force F_G as well as its entropic and biochemical components F_E and F_B, respectively, are shown as a function of w. The inset shows the variation using a linear scale for the forces and illustrates that F_B = 0 for w > 160 μm (regime I). To see this figure in color, go online.

Figure 6

Entropic ordering of a hard rod of length L in a channel of width w. (a) A sketch illustrating the states the hard rod assumes as it translates and reorients within channels of three different normalized widths $\overline{w}\equiv w/L$ is given. Rod orientation is denoted by ϕ. (b) Predictions of the orientational order parameter Θ_R as a function of $\overline{w}$ are shown for the FM (blue) in which the rod has translational and orientational degrees of freedom, the TC model (red), and the OC model (green), compared with the cell-order parameter from experimental data on stripe widths normalized by the average cell length 2${\ell }_{\text{e}}$. (c) Corresponding predictions of the total entropy S_T, orientational entropy S_ϕ, and translational entropy S_X for the three models as a function of $\overline{w}$ are shown. The discrete entropies plotted here are for the choices of the total number of available orientational and translational states N_ϕ = 314 and $1/\mathit{\Delta }\overline{w}=800$, respectively (see Supporting Materials and Methods, Section S4 for definitions). To see this figure in color, go online.