Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 May 21;116(21):10223-10225.
doi: 10.1073/pnas.1904139116. Epub 2019 May 6.

New Laplace and Helmholtz solvers

Abinand Gopal  1 , Lloyd N Trefethen  2
Affiliations

New Laplace and Helmholtz solvers

Abinand Gopal et al. Proc Natl Acad Sci U S A. .

Abstract

Numerical algorithms based on rational functions are introduced that solve the Laplace and Helmholtz equations on 2D domains with corners quickly and accurately, despite the corner singularities.

Keywords: Helmholtz equation; Laplace equation; rational functions; scattering.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.
Fig. 1.
Laplace equation in an L-shaped domain. Poles are clustered exponentially near vertices and a least-squares problem is solved on the boundary to find coefficients for a global representation [1] of the solution accurate to 10 digits. The black dot in the interior marks the point z* of [1]. The curve of maximal error on the boundary shows root-exponential convergence.
Fig. 2.
Fig. 2.
Helmholtz equation. Solutions to Δu+k2u=0 with k=50 in the exterior of a square (the real part is plotted). The incident signal on the left is a plane wave oriented at 30°, and on the right, a point oscillation H0(k|z−z0|) with z0=1/2+i.
See this image and copyright information in PMC

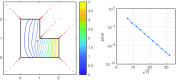
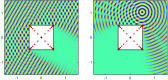
References

    1. Schwab C. p- and hp-Finite Element Methods. Clarendon; Oxford: 1999.
    1. Serkh K, Rokhlin V. On the solution of elliptic partial differential equations on regions with corners. J Comput Phys. 2016;305:150–171.
    1. Wasow W. Asymptotic development of the solution of Dirichlet’s problem at analytic corners. Duke Math J. 1957;24:47–56.
    1. Newman DJ. Rational approximation to |x|. Mich Math J. 1964;11:11–14.
    1. Hochman A, Leviatan Y, White JK. On the use of rational-function fitting methods for the solution of 2D Laplace boundary-value problems. J Comput Phys. 2013;238:337–358.

LinkOut - more resources