Mortality causes universal changes in microbial community composition
- PMID: 31073166
- PMCID: PMC6509412
- DOI: 10.1038/s41467-019-09925-0
Mortality causes universal changes in microbial community composition
Abstract
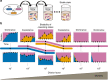
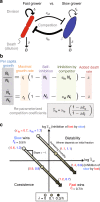
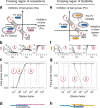
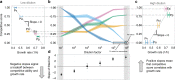
All organisms are sensitive to the abiotic environment, and a deteriorating environment can cause extinction. However, survival in a multispecies community depends upon interactions, and some species may even be favored by a harsh environment that impairs others, leading to potentially surprising community transitions as environments deteriorate. Here we combine theory and laboratory microcosms to predict how simple microbial communities will change under added mortality, controlled by varying dilution. We find that in a two-species coculture, increasing mortality favors the faster grower, confirming a theoretical prediction. Furthermore, if the slower grower dominates under low mortality, the outcome can reverse as mortality increases. We find that this tradeoff between growth and competitive ability is prevalent at low dilution, causing outcomes to shift dramatically as dilution increases, and that these two-species shifts propagate to simple multispecies communities. Our results argue that a bottom-up approach can provide insight into how communities change under stress.
Conflict of interest statement
The authors declare no competing interests.
Figures
References
-
- Tilman, D. Resource Competition and Community Structure (Princeton University Press, Princeton, NJ, 1982).
-
- Wellborn GA, Skelly DK, Werner EE. Mechanisms creating community structure across a freshwater habitat gradient. Annu. Rev. Ecol. Syst. 1996;27:337–363. doi: 10.1146/annurev.ecolsys.27.1.337. - DOI
-
- DÍez I, Secilla A, Santolaria A, Gorostiaga JM. Phytobenthic intertidal community structure along an environmental pollution gradient. Mar. Pollut. Bull. 1999;38:463–472. doi: 10.1016/S0025-326X(98)90161-8. - DOI
-
- Lessard JP, Sackett TE, Reynolds WN, Fowler DA, Sanders NJ. Determinants of the detrital arthropod community structure: the effects of temperature and resources along an environmental gradient. Oikos. 2011;120:333–343. doi: 10.1111/j.1600-0706.2010.18772.x. - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

