Rheology of Concentrated Polymer/Ionic Liquid Solutions: An Anomalous Plasticizing Effect and a Universality in Nonlinear Shear Rheology

Abstract

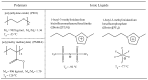
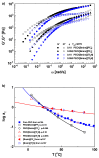
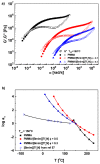
An anomalous plasticizing effect was observed in polymer/ionic liquid (IL) solutions by applying broad range of rheological techniques. Poly(ethylene oxide)(PEO)/IL solutions exhibit stronger dynamic temperature dependence than pure PEO, which is in conflict with the knowledge that lower-T_g solvent increases the fractional free volume. For poly(methy methacrylate)(PMMA)/IL solutions, the subtle anomaly was detected from the fact that the effective glass transition temperature T_g,eff of PMMA in IL is higher than the prediction of the self-concentration model, while in conventional polymer solutions, T_g,eff follows the original Fox equation. Observations in both solutions reveal retarded segmental dynamics, consistent with a recent simulation result (Macromolecules, 2018, 51, 5336) that polymer chains wrap the IL cations by hydrogen bonding interactions and the segmental unwrapping delays their relaxation. Start-up shear and nonlinear stress relaxation tests of polymer/IL solutions follow a universal nonlinear rheological behavior as polymer melts and solutions, indicating that the segment-cation interaction is not strong enough to influence the nonlinear chain orientation and stretch. The present work may arouse the further theoretical, experimental, and simulation interests in interpreting the effect of complex polymer-IL interaction on the dynamics of polymer/IL solutions.

Keywords: linear and nonlinear rheology; plasticizing effect; polymer/ionic liquid solution.

Scheme 1

Representative illustration showing that chain segments (PEO) wrap around the cations of ionic liquids ([Bmim][PF₆]) due to hydrogen bonding interaction.

Scheme 2

Structure, molecular weight, and T_g of PEO, PMMA, [Bmim][PF₆], and [Bmim][Tf₂N].

Figure 1

(a) Master curves of PEO in [Bmim][PF₆] and [Bmim][Tf₂N] at T_ref = 25 °C. (b) Horizontal shift factors a_T as function of temperature T with WLF fitting. (c) a_T as function of 1000/T with Arrhenius fitting, where the lower temperature limit for fitting is 45, 25 and 25 °C for PEO, PEO/[Bmim][PF₆], and PEO/[Bmim][Tf₂N], respectively.

Figure 1

(a) Master curves of PEO in [Bmim][PF₆] and [Bmim][Tf₂N] at T_ref = 25 °C. (b) Horizontal shift factors a_T as function of temperature T with WLF fitting. (c) a_T as function of 1000/T with Arrhenius fitting, where the lower temperature limit for fitting is 45, 25 and 25 °C for PEO, PEO/[Bmim][PF₆], and PEO/[Bmim][Tf₂N], respectively.

Figure 2

(a) The master curve, (b) the horizontal shift factor, and (c) the normalized terminal relaxation time τ_d/ϕ^2.0 for PMMA and its solutions in [Bmim][Tf₂N] at T_ref = 150 °C. (d) The effective glass transition temperatures as function of volume fraction ϕ for PMMA/[Bmim][Tf₂N] in this study (■) and PMMA/[Emim][Tf₂N] in ref [23] (▼,▽ for rheology and ●,○for DSC, unit k in legend representing kg/mol). The solid and dotted curves are predictions of LM model with self-concentration ϕ_self = 0 and 0.25, respectively. (e) ϕ_eff as a function of ϕ_ave for PMMA in IL solutions. The solid line is the diagonal representing ϕ_eff = ϕ_ave (or ϕ_self = 0), while he dotted curve is prediction of LM model with ϕ_self = 0.25. Also plotted are data for PVE/EHB (▲), PI/PHO (●), PS/toluene(◆), PS/TCP(◀), and simulated chain in good solvent (★), from ref [56].

Figure 2

(a) The master curve, (b) the horizontal shift factor, and (c) the normalized terminal relaxation time τ_d/ϕ^2.0 for PMMA and its solutions in [Bmim][Tf₂N] at T_ref = 150 °C. (d) The effective glass transition temperatures as function of volume fraction ϕ for PMMA/[Bmim][Tf₂N] in this study (■) and PMMA/[Emim][Tf₂N] in ref [23] (▼,▽ for rheology and ●,○for DSC, unit k in legend representing kg/mol). The solid and dotted curves are predictions of LM model with self-concentration ϕ_self = 0 and 0.25, respectively. (e) ϕ_eff as a function of ϕ_ave for PMMA in IL solutions. The solid line is the diagonal representing ϕ_eff = ϕ_ave (or ϕ_self = 0), while he dotted curve is prediction of LM model with ϕ_self = 0.25. Also plotted are data for PVE/EHB (▲), PI/PHO (●), PS/toluene(◆), PS/TCP(◀), and simulated chain in good solvent (★), from ref [56].

Figure 2

(a) The master curve, (b) the horizontal shift factor, and (c) the normalized terminal relaxation time τ_d/ϕ^2.0 for PMMA and its solutions in [Bmim][Tf₂N] at T_ref = 150 °C. (d) The effective glass transition temperatures as function of volume fraction ϕ for PMMA/[Bmim][Tf₂N] in this study (■) and PMMA/[Emim][Tf₂N] in ref [23] (▼,▽ for rheology and ●,○for DSC, unit k in legend representing kg/mol). The solid and dotted curves are predictions of LM model with self-concentration ϕ_self = 0 and 0.25, respectively. (e) ϕ_eff as a function of ϕ_ave for PMMA in IL solutions. The solid line is the diagonal representing ϕ_eff = ϕ_ave (or ϕ_self = 0), while he dotted curve is prediction of LM model with ϕ_self = 0.25. Also plotted are data for PVE/EHB (▲), PI/PHO (●), PS/toluene(◆), PS/TCP(◀), and simulated chain in good solvent (★), from ref [56].

Figure 3

Nonlinear startup shear viscosity η⁺ (thin curves) as a function of time for PMMA/[Bmim][Tf₂N] with ϕ = (a) 0.50 and (b) 0.30, for PEO/[Bmim][PF₆] with ϕ = (c) 0.10 and (d) 0.055, and for PEO/[Bmim][Tf₂N] with ϕ = (e) 0.10 and (f) 0.055. In each panel, the shear rates increase from top to bottom with a logarithmic interval of 0.5. The thick curves are LVE envelopes.

Figure 4

(a) Steady shear viscosities of PEO/IL solutions as a function of shear rate. The solid curves are from LVE results. (b) The maximum viscosity divided by steady viscosity η_max/η_steady, as a function of Rouse Weissenberg number Wi_R. (c) The strain where the maximum transient viscosity appears, γ_max, as a function of Wi_R. The legend for all panels: (■) PEO/[Bmim][PF₆], ϕ = 0.10, (●) PEO/[Bmim][Tf₂N], ϕ = 0.10, (□) PEO/[Bmim][PF₆], ϕ = 0.055, (○) PEO/[Bmim][Tf₂N], ϕ = 0.055, (◆) PMMA/[Bmim][Tf₂N], ϕ = 0.50, (◇) PMMA/[Bmim][Tf₂N], ϕ = 0.30, (△) PS-185 kg/mol (ref [33]), (▽) PS-133 kg/mol (ref [33]), (★) PS-285 kg/mol in PS-2 kg/mol solution, ϕ = 65% (ref [33]), (☆) PS-285 kg/mol in PS-2 kg/mol solution, ϕ= 47% (ref [33]), (∙∙∙∙∙) PS-200 kg/mol (ref [83]), (—) PI-30 kg/mol (ref [82]), (-----)PI-90 kg/mol (ref [82]), (×) PI (ref [84]).

Figure 4

(a) Steady shear viscosities of PEO/IL solutions as a function of shear rate. The solid curves are from LVE results. (b) The maximum viscosity divided by steady viscosity η_max/η_steady, as a function of Rouse Weissenberg number Wi_R. (c) The strain where the maximum transient viscosity appears, γ_max, as a function of Wi_R. The legend for all panels: (■) PEO/[Bmim][PF₆], ϕ = 0.10, (●) PEO/[Bmim][Tf₂N], ϕ = 0.10, (□) PEO/[Bmim][PF₆], ϕ = 0.055, (○) PEO/[Bmim][Tf₂N], ϕ = 0.055, (◆) PMMA/[Bmim][Tf₂N], ϕ = 0.50, (◇) PMMA/[Bmim][Tf₂N], ϕ = 0.30, (△) PS-185 kg/mol (ref [33]), (▽) PS-133 kg/mol (ref [33]), (★) PS-285 kg/mol in PS-2 kg/mol solution, ϕ = 65% (ref [33]), (☆) PS-285 kg/mol in PS-2 kg/mol solution, ϕ= 47% (ref [33]), (∙∙∙∙∙) PS-200 kg/mol (ref [83]), (—) PI-30 kg/mol (ref [82]), (-----)PI-90 kg/mol (ref [82]), (×) PI (ref [84]).

Figure 5

The stress relaxation moduli for (a) PMMA/[Bmim][Tf₂N], ϕ = 0.5, 160 °C, (b) PMMA/[Bmim][Tf₂N], ϕ = 0.3, 90 °C, (c) PEO/[Bmim][PF₆], ϕ = 0.10, 85 °C, (d) PEO/[Bmim][PF₆], ϕ = 0.055, 45 °C, (e) PEO/[Bmim][Tf₂N], ϕ = 0.10, 75 °C, and (f) PEO/[Bmim][Tf₂N], ϕ = 0.055, 25 °C. The solid curves are the G(t,γ) when γ→0, converted from master curves.

Figure 6

The stress relaxation moduli after vertical shifting for (a) PMMA/[Bmim][Tf₂N], ϕ = 0.5, 160 °C, (b) PMMA/[Bmim][Tf₂N], ϕ = 0.3, 90 °C, (c) PEO/[Bmim][PF₆], ϕ = 0.10, 85 °C, (d) PEO/[Bmim][PF₆], ϕ = 0.055, 45 °C, (e) PEO/[Bmim][Tf₂N], ϕ = 0.10, 75 °C, and (f) PEO/[Bmim][Tf₂N], ϕ = 0.055, 25 °C. Symbols are the same with Figure 5.

Figure 7

Damping functions of (■) PEO/[Bmim][PF₆], ϕ = 0.10, (●) PEO/[Bmim][Tf₂N], ϕ = 0.10, (□) PEO/[Bmim][PF₆], ϕ = 0.055, (○) PEO/[Bmim][Tf₂N], ϕ = 0.055, (◆) PMMA/[Bmim][Tf₂N], ϕ = 0.50, (◇) PMMA/[Bmim][Tf₂N], ϕ = 0.30, (▲) linear PS—84 kg/mol (ref [85]), (★) comb PS with diluted backbone entanglement number Z_diluted-bb = 4.42 (ref [102]), and (☆) comb PS with diluted backbone entanglement number Z_diluted-bb = 5.64 (ref [102]). The dotted curve is the Doi-Edwards prediction.