Structure and Hierarchy of Influenza Virus Models Revealed by Reaction Network Analysis
- PMID: 31100972
- PMCID: PMC6563504
- DOI: 10.3390/v11050449
Structure and Hierarchy of Influenza Virus Models Revealed by Reaction Network Analysis
Abstract
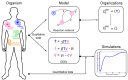
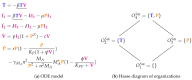
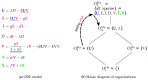
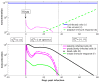
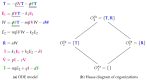
Influenza A virus is recognized today as one of the most challenging viruses that threatens both human and animal health worldwide. Understanding the control mechanisms of influenza infection and dynamics is crucial and could result in effective future treatment strategies. Many kinetic models based on differential equations have been developed in recent decades to capture viral dynamics within a host. These models differ in their complexity in terms of number of species elements and number of reactions. Here, we present a new approach to understanding the overall structure of twelve influenza A virus infection models and their relationship to each other. To this end, we apply chemical organization theory to obtain a hierarchical decomposition of the models into chemical organizations. The decomposition is based on the model structure (reaction rules) but is independent of kinetic details such as rate constants. We found different types of model structures ranging from two to eight organizations. Furthermore, the model's organizations imply a partial order among models entailing a hierarchy of model, revealing a high model diversity with respect to their long-term behavior. Our methods and results can be helpful in model development and model integration, also beyond the influenza area.
Keywords: chemical organization theory; complex networks analysis; influenza A; virus dynamics modeling.
Conflict of interest statement
The authors declare no conflict of interest
Figures
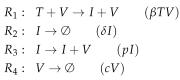

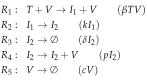


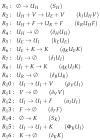
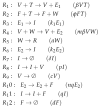
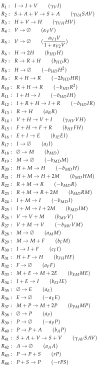
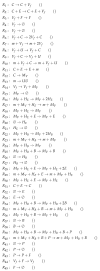
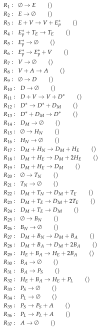

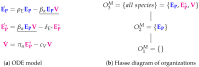


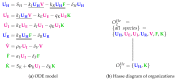





Similar articles
-
Structure and Hierarchy of SARS-CoV-2 Infection Dynamics Models Revealed by Reaction Network Analysis.Viruses. 2020 Dec 23;13(1):14. doi: 10.3390/v13010014. Viruses. 2020. PMID: 33374824 Free PMC article.
-
Innate Immunity and the Inter-exposure Interval Determine the Dynamics of Secondary Influenza Virus Infection and Explain Observed Viral Hierarchies.PLoS Comput Biol. 2015 Aug 18;11(8):e1004334. doi: 10.1371/journal.pcbi.1004334. eCollection 2015 Aug. PLoS Comput Biol. 2015. PMID: 26284917 Free PMC article.
-
Modelling the Effect of MUC1 on Influenza Virus Infection Kinetics and Macrophage Dynamics.Viruses. 2021 May 7;13(5):850. doi: 10.3390/v13050850. Viruses. 2021. PMID: 34066999 Free PMC article.
-
[Bioinformatics technologies for the analysis of antigenic evolution of influenza viruses].Uirusu. 2011 Jun;61(1):3-13. doi: 10.2222/jsv.61.3. Uirusu. 2011. PMID: 21972551 Review. Japanese.
-
Cross talk between animal and human influenza viruses.Annu Rev Anim Biosci. 2013 Jan;1:21-42. doi: 10.1146/annurev-animal-031412-103733. Epub 2013 Jan 1. Annu Rev Anim Biosci. 2013. PMID: 25387011 Free PMC article. Review.
Cited by
-
Structure and Hierarchy of SARS-CoV-2 Infection Dynamics Models Revealed by Reaction Network Analysis.Viruses. 2020 Dec 23;13(1):14. doi: 10.3390/v13010014. Viruses. 2020. PMID: 33374824 Free PMC article.
-
Phylogenetic Insights into H7Nx Influenza Viruses: Uncovering Reassortment Patterns and Geographic Variability.Viruses. 2024 Oct 23;16(11):1656. doi: 10.3390/v16111656. Viruses. 2024. PMID: 39599771 Free PMC article.
-
Revealing the hierarchical structure of microbial communities.Sci Rep. 2024 May 16;14(1):11202. doi: 10.1038/s41598-024-61836-3. Sci Rep. 2024. PMID: 38755262 Free PMC article.
-
Trends in mathematical modeling of host-pathogen interactions.Cell Mol Life Sci. 2020 Feb;77(3):467-480. doi: 10.1007/s00018-019-03382-0. Epub 2019 Nov 27. Cell Mol Life Sci. 2020. PMID: 31776589 Free PMC article. Review.
-
Computing all persistent subspaces of a reaction-diffusion system.Sci Rep. 2023 Oct 11;13(1):17169. doi: 10.1038/s41598-023-44244-x. Sci Rep. 2023. PMID: 37821664 Free PMC article.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

