A Flexible Model of Working Memory
- PMID: 31103359
- PMCID: PMC6613943
- DOI: 10.1016/j.neuron.2019.04.020
A Flexible Model of Working Memory
Abstract
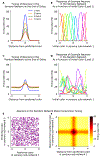
Working memory is fundamental to cognition, allowing one to hold information "in mind." A defining characteristic of working memory is its flexibility: we can hold anything in mind. However, typical models of working memory rely on finely tuned, content-specific attractors to persistently maintain neural activity and therefore do not allow for the flexibility observed in behavior. Here, we present a flexible model of working memory that maintains representations through random recurrent connections between two layers of neurons: a structured "sensory" layer and a randomly connected, unstructured layer. As the interactions are untuned with respect to the content being stored, the network maintains any arbitrary input. However, in our model, this flexibility comes at a cost: the random connections overlap, leading to interference between representations and limiting the memory capacity of the network. Additionally, our model captures several other key behavioral and neurophysiological characteristics of working memory.
Keywords: capacity limitations; cognitive control; cognitive flexibility; computational model; excitation-inhibition balance; mixed selectivity; working memory.
Copyright © 2019 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Interests
The authors declare no competing interests.
Figures






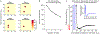
Comment in
-
Working Memory: Flexible but Finite.Neuron. 2019 Jul 17;103(2):184-185. doi: 10.1016/j.neuron.2019.06.025. Neuron. 2019. PMID: 31319047 Free PMC article.
References
-
- Barak O, Tsodyks M, 2014. Working models of working memory. Current opinion in neurobiology 25, 20–24. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

