Multifractal Desynchronization of the Cardiac Excitable Cell Network During Atrial Fibrillation. II. Modeling
- PMID: 31105585
- PMCID: PMC6492055
- DOI: 10.3389/fphys.2019.00480
Multifractal Desynchronization of the Cardiac Excitable Cell Network During Atrial Fibrillation. II. Modeling
Abstract
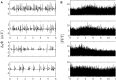
In a companion paper (I. Multifractal analysis of clinical data), we used a wavelet-based multiscale analysis to reveal and quantify the multifractal intermittent nature of the cardiac impulse energy in the low frequency range ≲ 2Hz during atrial fibrillation (AF). It demarcated two distinct areas within the coronary sinus (CS) with regionally stable multifractal spectra likely corresponding to different anatomical substrates. The electrical activity also showed no sign of the kind of temporal correlations typical of cascading processes across scales, thereby indicating that the multifractal scaling is carried by variations in the large amplitude oscillations of the recorded bipolar electric potential. In the present study, to account for these observations, we explore the role of the kinetics of gap junction channels (GJCs), in dynamically creating a new kind of imbalance between depolarizing and repolarizing currents. We propose a one-dimensional (1D) spatial model of a denervated myocardium, where the coupling of cardiac cells fails to synchronize the network of cardiac cells because of abnormal transjunctional capacitive charging of GJCs. We show that this non-ohmic nonlinear conduction 1D modeling accounts quantitatively well for the "multifractal random noise" dynamics of the electrical activity experimentally recorded in the left atrial posterior wall area. We further demonstrate that the multifractal properties of the numerical impulse energy are robust to changes in the model parameters.
Keywords: atrial fibrillation; excitable cell network; intermittent dynamics; kinetics of gap junction channel; modeling; multifractal analysis.
Figures





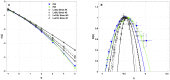
 ) (in δx = 0.3 mm units). The curves correspond to quadratic spectra (Equations 23 and 24) with parameters [c0, c1, c2] reported in Table 3. For comparison are reported the spectra previously obtained from the experimental time-series recorded at the electrodes Pt3 (blue ▼) and Pt5 (green ▼) in the left atrial posterior wall (Companion paper I Attuel et al., 2017).
) (in δx = 0.3 mm units). The curves correspond to quadratic spectra (Equations 23 and 24) with parameters [c0, c1, c2] reported in Table 3. For comparison are reported the spectra previously obtained from the experimental time-series recorded at the electrodes Pt3 (blue ▼) and Pt5 (green ▼) in the left atrial posterior wall (Companion paper I Attuel et al., 2017).

 ) (in δx = 0.3 mm units). The curves correspond to quadratic spectra (Equations 23 and 24) with parameters [c0, c1, c2] reported in Table 5. For comparison are reported in open symbols (◦, □, ▽ △), the corresponding spectra previously obtained with the set of parameter values defined in Simul #2 (Table 1) and L = 150 in Figure 5.
) (in δx = 0.3 mm units). The curves correspond to quadratic spectra (Equations 23 and 24) with parameters [c0, c1, c2] reported in Table 5. For comparison are reported in open symbols (◦, □, ▽ △), the corresponding spectra previously obtained with the set of parameter values defined in Simul #2 (Table 1) and L = 150 in Figure 5.
References
-
- Arneodo A., Audit B., Decoster N., Muzy J.-F., Vaillant C. (2002). A wavelet based multifractal formalism: application to DNA sequences, satellite images of the cloud structure and stock market data, in The Science of Disasters: Climate Disruptions, Heart Attacks, and Market Crashes, eds Bunde A., Kropp J., Schellnhuber H. J. (Berlin: Springer Verlag; ), 26–102.
-
- Arneodo A., Audit B., Kestener P., Roux S. G. (2008). Wavelet-based multifractal analysis. Scholarpedia 3:4103 10.4249/scholarpedia.4103 - DOI
-
- Arneodo A., Bacry E., Jaffard S., Muzy J.-F. (1997). Oscillating singularities on Cantor sets: a grand-canonical multifractal formalism. J. Stat. Phys. 87, 179–209. 10.1007/BF02181485 - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

