Machine Learning of Coarse-Grained Molecular Dynamics Force Fields

Abstract

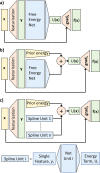
Atomistic or ab initio molecular dynamics simulations are widely used to predict thermodynamics and kinetics and relate them to molecular structure. A common approach to go beyond the time- and length-scales accessible with such computationally expensive simulations is the definition of coarse-grained molecular models. Existing coarse-graining approaches define an effective interaction potential to match defined properties of high-resolution models or experimental data. In this paper, we reformulate coarse-graining as a supervised machine learning problem. We use statistical learning theory to decompose the coarse-graining error and cross-validation to select and compare the performance of different models. We introduce CGnets, a deep learning approach, that learns coarse-grained free energy functions and can be trained by a force-matching scheme. CGnets maintain all physically relevant invariances and allow one to incorporate prior physics knowledge to avoid sampling of unphysical structures. We show that CGnets can capture all-atom explicit-solvent free energy surfaces with models using only a few coarse-grained beads and no solvent, while classical coarse-graining methods fail to capture crucial features of the free energy surface. Thus, CGnets are able to capture multibody terms that emerge from the dimensionality reduction.

Figure 1

Typical bias–variance trade-off for fixed data set size, indicating the balance between underfitting and overfitting. The noise level is defined by the CG scheme (i.e., which particles are kept and which are discarded) and is the lower bound for the mean prediction error.

Figure 2

Neural network schemes. (a) CGnet. (b) Regularized CGnet with prior energy. (c) Spline model representing a standard CG approach, for comparison. Each energy term is a function of only one feature, and the features are defined as all the bonds, angles, dihedrals, and nonbonded pairs of atoms.

Figure 3

Machine-learned coarse-graining of dynamics in a rugged 2D potential. (a) Two-dimensional potential used as a toy system. (b) Exact free energy along x. (c) Instantaneous forces and the learned mean forces using feature regression and CGnet models (regularized and unregularized) compared to the exact forces. The unit of the force is k_BT, with the unit of length equal to 1. (d) Free energy (PMF) along x predicted using feature regression, and CGnet models compared to the exact free energy. Free energies are also computed from histogramming simulation data directly, using the underlying 2D trajectory, or simulations run with the feature regression and CGnet models (dashed lines).

Figure 4

Mapping of alanine dipeptide from an all-atom solvated model (top) to a CG model consisting of the five central backbone atoms (bottom).

Figure 5

(a–c) Cross-validated force-matching error in [kcal/(mol A)]² for the selection of the optimum structure of the network. (d–f) Difference between the two-dimensional free energy surfaces obtained from the CG models and from the reference all-atom simulations (see Figure 6) for the regularized CGnet and the spline model of alanine dipeptide. (a) Selection of the number of layers, D. (b) Selection of the number of neurons per layer, W. (c) Selection of the Lipschitz regularization strength, λ. The selected hyperparameters, corresponding to the smallest cross-validation error, are highlighted by orange boxes. Blue dashed lines represent the regularized CGnet, red dashed lines the spline model, and vertical bars the standard error of the mean. (d–f) Difference between the reference all-atom free energy surface and the free energy surfaces corresponding to the choices of hyperparameters indicated in panels a–c as (C1, C2, C3, C4, C5) for CGnet and as (S1, S2, S3, S4) for the spline model.

Figure 6

Free energy profiles and simulated structures of alanine dipeptide using all-atom and machine-learned coarse-grained models. (a) Reference free energy as a function of the dihedral angles, as obtained from direct histogram estimation from all-atom simulation. (b) Standard coarse-grained model using a sum of splines of individual internal coordinates. (c) Regularized CGnet as proposed here. (d) Unregularized CGnet. (e) Representative structures in the six free energy minima, from atomistic simulation (ball-and-stick representation) and regularized CGnet simulation (licorice representation).

Figure 7

Free energy landscape of Chignolin for the different models. (a) Free energy as obtained from all-atom simulation, as a function of the first two TICA coordinates. (b) Free energy as obtained from the spline model, as a function of the same two coordinates used in the all-atom model. (c) Free energy as obtained from CGnet, as a function of the same two coordinates. (d) Comparison of the one-dimensional free energy as a function of the first TICA coordinate (corresponding to the folding/unfolding transition) for the three models: all-atom (blue), spline (green), and CGnet (red). (e) Representative Chignolin configurations in the three minima from (a–c) all-atom simulation and (a′–c′) CGnet.