Thermally Fully Developed Electroosmotic Flow of Power-Law Nanofluid in a Rectangular Microchannel

Abstract

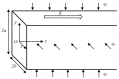
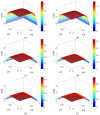
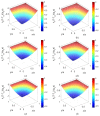
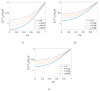
The hydrodynamic and thermal behavior of the electroosmotic flow of power-law nanofluid is studied. A modified Cauchy momentum equation governing the hydrodynamic behavior of power-law nanofluid flow in a rectangular microchannel is firstly developed. To explore the thermal behavior of power-law nanofluid flow, the energy equation is developed, which is coupled to the velocity field. A numerical algorithm based on the Crank-Nicolson method and compact difference schemes is proposed, whereby the velocity, temperature, and Nusselt number are computed for different parameters. A larger nanoparticle volume fraction significantly reduces the velocity and enhances the temperature regardless of the base fluid rheology. The Nusselt number increases with the flow behavior index and with electrokinetic width when considering the surface heating effect, which decreases with the Joule heating parameter. The heat transfer rate of electroosmotic flow is enhanced for shear thickening nanofluids or at a greater nanoparticle volume fraction.

Keywords: Joule heating parameter; compact difference scheme; electroosmotic flow; heat transfer; nanoparticle volume friction; power-law nanofluid.

Figure 1

Sketch of the rectangular microchannel with height 2a, width 2b, and constant heat flux q_s at the walls.

Figure 2

The comparison between the numerical solution and analytical solution from for (a) velocity distribution at $\overline{y}=0$ and (b) temperature distribution at $\overline{y}=0$.

Figure 3

The comparison among the velocity distributions of shear thinning nanofluid, Newtonian nanofluid and shear thickening nanofluid at different nanoparticle volume fraction: (a) ϕ = 0, n = 0.8; (b) ϕ = 0.06, n = 0.8; (c) ϕ = 0, n = 1.0; (d) ϕ = 0.06, n = 1.0; (e) ϕ = 0, n = 1.2; (f) ϕ = 0.06, n = 1.2.

Figure 4

The dimensionless temperature distributions of shear thinning fluid, Newtonian fluid, and shear thickening fluid for different Joule heating parameter when nanoparticle volume fraction is ϕ = 0: (a) n = 0.8, S = 0; (b) n = 0.8, S = 3; (c) n = 1.0, S = 0; (d) n = 1.0, S = 3; (e) n = 1.2, S = 0; (f) n = 1.2, S = 3.

Figure 5

The dimensionless temperature distributions of shear thinning nanofluid, Newtonian nanofluid, and shear thickening nanofluid for different Joule heating parameters S when nanoparticle volume fraction is ϕ = 0.06: (a) n = 0.8, S = 0; (b) n = 0.8, S = 3; (c) n = 1.0, S = 0; (d) n = 1.0, S = 3; (e) n = 1.2, S = 0; (f) n = 1.2, S = 3.

Figure 6

The comparison among temperature profiles at $\overline{y}=0$ for different nanoparticle volume fractions ϕ in the case of (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.

Figure 7

The comparison among temperature profiles at $\overline{y}=0$ for different Joule heating parameters in the case of (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.

Figure 8

The variation of Nusselt number with the electrokinetic width K for shear thinning nanofluid, Newtonian nanofluid, shear thickening nanofluid when the Joule heating parameters are given as (a) S = −5; (b) S = 0; (c) S = 5.

Figure 9

The variation of Nusselt number with Joule heating parameter for shear thinning nanofluid, Newtonian nanofluid, and shear thickening nanofluid in the case of (a) ϕ = 0 and (b) ϕ = 0.06.

Figure 10

The variation of (a) Nusselt number and (b) Bejan number with flow behavior index for different nanoparticle volume fraction.