Robust approach for rotor mapping in cardiac tissue

Abstract

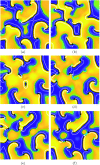
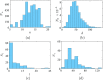
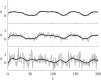
The motion of and interaction between phase singularities that lie at the centers of spiral waves capture many qualitative and, in some cases, quantitative features of complex dynamics in excitable systems. Being able to accurately reconstruct their position is thus quite important, even if the data are noisy and sparse, as in electrophysiology studies of cardiac arrhythmias, for instance. A recently proposed global topological approach [Marcotte and Grigoriev, Chaos 27, 093936 (2017)] promises to meaningfully improve the quality of the reconstruction compared with traditional, local approaches. Indeed, we found that this approach is capable of handling noise levels exceeding the range of the signal with minimal loss of accuracy. Moreover, it also works successfully with data sampled on sparse grids with spacing comparable to the mean separation between the phase singularities for complex patterns featuring multiple interacting spiral waves.

FIG. 1.

Comparison of sets ${\ell }^k$ (a) and ${\overline{\ell }}^k$ (b) for noiseless data, with $k=1$ in black and $k=2$ in gray. The domain is $256\times 256$ grid points. Panel (a) contains a number of artifacts, which have to do with a characteristic feature of most cardiac models, namely, very flat repolarization plateaus.

FIG. 2.

The signed distance $d_s^1$ (black) and its smoothed version ${\overline{d}}_s^1$ (gray) at a fixed time over a $j=\mathrm{constant}$ slice of the domain.

FIG. 3.

Snapshots of benchmark data [colorbar is shown in Fig. 7(a)] equally spaced in time over 56 frames (approximately one rotation period), with curves ${\overline{\ell }}^1$ (white) and ${\overline{\ell }}^2$ (black) and PSs superimposed. Here and below, solid and dashed white segments correspond to the leading and trailing edges of the refractory region, respectively; solid and dashed black correspond to the wavefront and waveback. PSs with chirality $+1$ and $-1$ are, respectively, shown as black and white circles. The $x$($y$) axis is horizontal (vertical). A full movie is provided in the supplementary material.

FIG. 4.

Trajectories of PSs with lifetimes of at least one period during the same time interval as shown in Fig. 3. Thicker curves correspond to PSs created during this period.

FIG. 5.

PS statistics. (a) Histogram of the total number $n$ of PSs in each frame. (b) Histogram of the distance $d$ from each PS to the nearest PS of opposite chirality, computed separately for each PS in each frame. (c) Histogram of the lifetime $l$ in periods of each PS. (d) Histogram of the separation $r$ between the most distant pair of points along the trajectory of each PS.

FIG. 6.

A typical time trace of the voltage signal before (gray) and after (black) temporal smoothing for different noise levels (from top to bottom, $\eta =0.1$, $\eta =0.3$, and $\eta =1$).

FIG. 7.

The frame shown in Fig. 3(c) with four different levels of added noise ($\eta =0,0.1,0.3,1$); overlaid are the curves ${\overline{\ell }}^1$ and ${\overline{\ell }}^2$ and PSs computed from the noisy data in each case.

FIG. 8.

The frame shown in Fig. 3(c) after interpolating from four levels of sparsification: (a) spatial resolution $256\times 256$ (same as benchmark), (b) $32\times 32$, (c) $16\times 16$, and (d) $8\times 8$. As in the previous figure, the curves ${\overline{\ell }}^1$ and ${\overline{\ell }}^2$ and PSs computed from the sparsified data are overlaid.