A Brownian Ratchet Model Explains the Biased Sidestepping of Single-Headed Kinesin-3 KIF1A
- PMID: 31155147
- PMCID: PMC6588830
- DOI: 10.1016/j.bpj.2019.05.011
A Brownian Ratchet Model Explains the Biased Sidestepping of Single-Headed Kinesin-3 KIF1A
Abstract
The kinesin-3 motor KIF1A is involved in long-ranged axonal transport in neurons. To ensure vesicular delivery, motors need to navigate the microtubule lattice and overcome possible roadblocks along the way. The single-headed form of KIF1A is a highly diffusive motor that has been shown to be a prototype of a Brownian motor by virtue of a weakly bound diffusive state to the microtubule. Recently, groups of single-headed KIF1A motors were found to be able to sidestep along the microtubule lattice, creating left-handed helical membrane tubes when pulling on giant unilamellar vesicles in vitro. A possible hypothesis is that the diffusive state enables the motor to explore the microtubule lattice and switch protofilaments, leading to a left-handed helical motion. Here, we study the longitudinal rotation of microtubules driven by single-headed KIF1A motors using fluorescence-interference contrast microscopy. We find an average rotational pitch of ≃1.5μm, which is remarkably robust to changes in the gliding velocity, ATP concentration, microtubule length, and motor density. Our experimental results are compared to stochastic simulations of Brownian motors moving on a two-dimensional continuum ratchet potential, which quantitatively agree with the fluorescence-interference contrast experiments. We find that single-headed KIF1A sidestepping can be explained as a consequence of the intrinsic handedness and polarity of the microtubule lattice in combination with the diffusive mechanochemical cycle of the motor.
Copyright © 2019 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
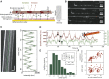


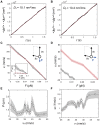
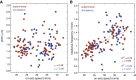
References
-
- Howard J. Sinauer Associates; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton.
- Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton: Sinauer Associates, Sunderland, MA.
-
- Alberts B., Johnson A., Walter P. Garland; New York: 1994. Molecular Biology of the Cell.
- Alberts, B., A. Johnson, …, P. Walter. 1994. Molecular Biology of the Cell: Garland, New York.
-
- Brunnbauer M., Dombi R., Ökten Z. Torque generation of kinesin motors is governed by the stability of the neck domain. Mol. Cell. 2012;46:147–158. - PubMed
- Brunnbauer, M., R. Dombi, …, Z. Okten. 2012. Torque generation of kinesin motors is governed by the stability of the neck domain. Mol. Cell. 46:147-158. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

