Coding Capacity of Purkinje Cells With Different Schemes of Morphological Reduction
- PMID: 31156415
- PMCID: PMC6530636
- DOI: 10.3389/fncom.2019.00029
Coding Capacity of Purkinje Cells With Different Schemes of Morphological Reduction
Abstract
The brain as a neuronal system has very complex structures with a large diversity of neuronal types. The most basic complexity is seen from the structure of neuronal morphology, which usually has a complex tree-like structure with dendritic spines distributed in branches. To simulate a large-scale network with spiking neurons, the simple point neuron, such as the integrate-and-fire neuron, is often used. However, recent experimental evidence suggests that the computational ability of a single neuron is largely enhanced by its morphological structure, in particular, by various types of dendritic dynamics. As the morphology reduction of detailed biophysical models is a classic question in systems neuroscience, much effort has been taken to simulate a neuron with a few compartments to include the interaction between the soma and dendritic spines. Yet, novel reduction methods are still needed to deal with the complex dendritic tree. Here, using 10 individual Purkinje cells of the cerebellum from three species of guinea-pig, mouse and rat, we consider four types of reduction methods and study their effects on the coding capacity of Purkinje cells in terms of firing rate, timing coding, spiking pattern, and modulated firing under different stimulation protocols. We found that there is a variation of reduction performance depending on individual cells and species, however, all reduction methods can preserve, to some degree, firing activity of the full model of Purkinje cell. Therefore, when stimulating large-scale network of neurons, one has to choose a proper type of reduced neuronal model depending on the questions addressed. Among these reduction schemes, Branch method, that preserves the geometrical volume of neurons, can achieve the best balance among different performance measures of accuracy, simplification, and computational efficiency, and reproduce various phenomena shown in the full morphology model of Purkinje cells. Altogether, these results suggest that the Branch reduction scheme seems to provide a general guideline for reducing complex morphology into a few compartments without the loss of basic characteristics of the firing properties of neurons.
Keywords: Purkinje cell; dendritic model; multi-compartmental models; neuronal morphology; rate coding; temporal coding.
Figures

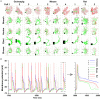



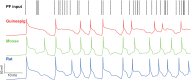



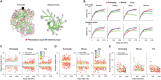
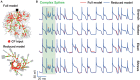
Similar articles
-
Virtual NEURON: a strategy for merged biochemical and electrophysiological modeling.J Comput Neurosci. 2011 Oct;31(2):385-400. doi: 10.1007/s10827-011-0317-0. Epub 2011 Feb 22. J Comput Neurosci. 2011. PMID: 21340454 Free PMC article.
-
The Cellular Electrophysiological Properties Underlying Multiplexed Coding in Purkinje Cells.J Neurosci. 2021 Mar 3;41(9):1850-1863. doi: 10.1523/JNEUROSCI.1719-20.2020. Epub 2021 Jan 15. J Neurosci. 2021. PMID: 33452223 Free PMC article.
-
Neuronal Atrophy Early in Degenerative Ataxia Is a Compensatory Mechanism to Regulate Membrane Excitability.J Neurosci. 2015 Aug 12;35(32):11292-307. doi: 10.1523/JNEUROSCI.1357-15.2015. J Neurosci. 2015. PMID: 26269637 Free PMC article.
-
Generation, description and storage of dendritic morphology data.Philos Trans R Soc Lond B Biol Sci. 2001 Aug 29;356(1412):1131-45. doi: 10.1098/rstb.2001.0905. Philos Trans R Soc Lond B Biol Sci. 2001. PMID: 11545695 Free PMC article. Review.
-
Using realistic models to study synaptic integration in cerebellar Purkinje cells.Rev Neurosci. 1999;10(3-4):233-45. doi: 10.1515/revneuro.1999.10.3-4.233. Rev Neurosci. 1999. PMID: 10526889 Review.
Cited by
-
Dissecting cascade computational components in spiking neural networks.PLoS Comput Biol. 2021 Nov 29;17(11):e1009640. doi: 10.1371/journal.pcbi.1009640. eCollection 2021 Nov. PLoS Comput Biol. 2021. PMID: 34843460 Free PMC article.
-
Transcranial direct current stimulation of cerebellum alters spiking precision in cerebellar cortex: A modeling study of cellular responses.PLoS Comput Biol. 2021 Dec 9;17(12):e1009609. doi: 10.1371/journal.pcbi.1009609. eCollection 2021 Dec. PLoS Comput Biol. 2021. PMID: 34882680 Free PMC article.
-
Modulation of the dynamics of cerebellar Purkinje cells through the interaction of excitatory and inhibitory feedforward pathways.PLoS Comput Biol. 2021 Feb 10;17(2):e1008670. doi: 10.1371/journal.pcbi.1008670. eCollection 2021 Feb. PLoS Comput Biol. 2021. PMID: 33566820 Free PMC article.
-
Diverse role of NMDA receptors for dendritic integration of neural dynamics.PLoS Comput Biol. 2023 Apr 10;19(4):e1011019. doi: 10.1371/journal.pcbi.1011019. eCollection 2023 Apr. PLoS Comput Biol. 2023. PMID: 37036844 Free PMC article.
-
Regulating synchronous oscillations of cerebellar granule cells by different types of inhibition.PLoS Comput Biol. 2021 Jun 28;17(6):e1009163. doi: 10.1371/journal.pcbi.1009163. eCollection 2021 Jun. PLoS Comput Biol. 2021. PMID: 34181653 Free PMC article.
References
LinkOut - more resources
Full Text Sources
Research Materials

