Modeling longitudinal imaging biomarkers with parametric Bayesian multi-task learning

Abstract

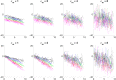
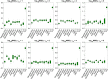
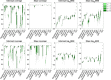
Longitudinal imaging biomarkers are invaluable for understanding the course of neurodegeneration, promising the ability to track disease progression and to detect disease earlier than cross-sectional biomarkers. To properly realize their potential, biomarker trajectory models must be robust to both under-sampling and measurement errors and should be able to integrate multi-modal information to improve trajectory inference and prediction. Here we present a parametric Bayesian multi-task learning based approach to modeling univariate trajectories across subjects that addresses these criteria. Our approach learns multiple subjects' trajectories within a single model that allows for different types of information sharing, that is, coupling, across subjects. It optimizes a combination of uncoupled, fully coupled and kernel coupled models. Kernel-based coupling allows linking subjects' trajectories based on one or more biomarker measures. We demonstrate this using Alzheimer's Disease Neuroimaging Initiative (ADNI) data, where we model longitudinal trajectories of MRI-derived cortical volumes in neurodegeneration, with coupling based on APOE genotype, cerebrospinal fluid (CSF) and amyloid PET-based biomarkers. In addition to detecting established disease effects, we detect disease related changes within the insula that have not received much attention within the literature. Due to its sensitivity in detecting disease effects, its competitive predictive performance and its ability to learn the optimal parameter covariance from data rather than choosing a specific set of random and fixed effects a priori, we propose that our model can be used in place of or in addition to linear mixed effects models when modeling biomarker trajectories. A software implementation of the method is publicly available.

Keywords: Alzheimer's disease; Bayesian analysis; biomarkers; longitudinal analysis; machine learning; multimodal analysis; structural MRI.

Figure 1

Top row: One run of the simulation of 200 subjects' longitudinal samples with group differences in intercept at four different measurement noise (σ_m) levels. Bottom row: The same with group differences in slope. Each subject has three samples, with trajectory parameters chosen from among five gradations of intercept (top row) or slope (bottom row), indicated by different colors [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 2

Boxplots of log mean absolute errors (MAEs) of predictions of all models across all simulations runs for the two scenarios: intercept variation (top row) and slope variation (bottom row) for four levels of measurement noise (σ_m). Models with oracle‐like prior information are marked with an asterisk (top row: "int" models; bottom row: "slope" models) [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 3

Boxplots of parameter coverage probabilities (i.e., fractions of times the true parameter value fell within the posterior credible region) and log mean absolute errors (MAE) between estimated and actual parameters for the two scenarios: intercept variation (top row) and slope variation (bottom row) for four measurement noise levels (σ_m). Models with oracle‐like prior information are marked with an asterisk (top row: "int" models; bottom row: "slope" models) [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4

Top: True and estimated annualized rates of change across cortex for four representative MTL models bottom: MAEs of estimates. MAE, mean absolute error [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5

Log Bayes factors across cortex, comparing each biomarker‐coupled MTL model to “random” [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6

Top: Significance of (cross‐sectional) diagnostic group differences in predicted volume at mean baseline age (73.5 years) for OLS, LME, and selected MTL models bottom: same for (longitudinal) group differences in estimated slopes [Color figure can be viewed at http://wileyonlinelibrary.com]