Accurate Estimation of Neural Population Dynamics without Spike Sorting
- PMID: 31171448
- PMCID: PMC7002296
- DOI: 10.1016/j.neuron.2019.05.003
Accurate Estimation of Neural Population Dynamics without Spike Sorting
Abstract
A central goal of systems neuroscience is to relate an organism's neural activity to behavior. Neural population analyses often reduce the data dimensionality to focus on relevant activity patterns. A major hurdle to data analysis is spike sorting, and this problem is growing as the number of recorded neurons increases. Here, we investigate whether spike sorting is necessary to estimate neural population dynamics. The theory of random projections suggests that we can accurately estimate the geometry of low-dimensional manifolds from a small number of linear projections of the data. We recorded data using Neuropixels probes in motor cortex of nonhuman primates and reanalyzed data from three previous studies and found that neural dynamics and scientific conclusions are quite similar using multiunit threshold crossings rather than sorted neurons. This finding unlocks existing data for new analyses and informs the design and use of new electrode arrays for laboratory and clinical use.
Keywords: brain computer interface; dimensionality reduction; neural dynamics; neural implant; neural signal processing; neural trajectories; neurophysiology; random projections; spike sorting.
Copyright © 2019 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Interests
K.V.S. is a consultant to CTRL-Labs and Neuralink Inc. and on the Scientific Advisory Boards of Cognescent and Heal; these entities in no way influenced or supported this work.
Figures




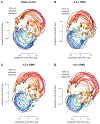
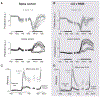

Comment in
-
Low Dimensionality, High Robustness in Neural Population Dynamics.Neuron. 2019 Jul 17;103(2):177-179. doi: 10.1016/j.neuron.2019.06.021. Neuron. 2019. PMID: 31319044
References
-
- Advani M, Lahiri S, & Ganguli S (2013). Statistical mechanics of complex neural systems and high dimensional data. J. Stat. Mech, 2013, P03014.
-
- Ajiboye AB, Willett FR, Young DR, Memberg WD, Murphy BA, Miller JP, Walter BL, Sweet JA, Hoyen HA, Keith MW, Peckham PH, Simeral JD, Donoghue JP, Hochberg LR, & Kirsch RF (2017). Restoration of reaching and grasping movements through brain-controlled muscle stimulation in a person with tetraplegia: a proof-of-concept demonstration. Lancet, 389, 1821–1830. - PMC - PubMed
-
- Baraniuk RG & Wakin MB (2009). Random projections of smooth manifolds. Foundations of Computational Mathematics, 9, 51–77.
-
- Bargmann C, Newsome W, Anderson A, Brown E, Deisseroth K, Donoghue J, MacLeish P, Marder E, Normann R, Sanes J, & Others (2014). BRAIN 2025: a scientific vision. Brain Research Through Advancing Innovative Neurotechnologies (BRAIN) Working Group Report to the Advisory Committee to the Director, NIH. Available online at: http://www.nih.gov/science/brain/2025/(US National Institutes of Health, 2014).
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

