Stein's method and approximating the quantum harmonic oscillator
- PMID: 31178654
- PMCID: PMC6550468
- DOI: 10.3150/17-BEJ960
Stein's method and approximating the quantum harmonic oscillator
Abstract
Hall et al. (2014) recently proposed that quantum theory can be understood as the continuum limit of a deterministic theory in which there is a large, but finite, number of classical "worlds." A resulting Gaussian limit theorem for particle positions in the ground state, agreeing with quantum theory, was conjectured in Hall et al. (2014) and proven by McKeague and Levin (2016) using Stein's method. In this article we show how quantum position probability densities for higher energy levels beyond the ground state may arise as distributional fixed points in a new generalization of Stein's method These are then used to obtain a rate of distributional convergence for conjectured particle positions in the first energy level above the ground state to the (two-sided) Maxwell distribution; new techniques must be developed for this setting where the usual "density approach" Stein solution (see Chatterjee and Shao (2011)) has a singularity.
Keywords: Higher energy levels; Interacting particle system; Maxwell distribution; Stein’s method.
Figures
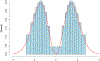
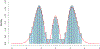
References
-
- Bohm D (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 85, 166–179.
-
- Cacoullos T and Papathanasiou V (1989). Characterizations of distributions by variance bounds. Statist. Probab. Lett. 7, 351–356.
-
- Chatterjee S (2009). Fluctuations of eigenvalues and second order Poincaré inequalities. Probab. Theory Related Fields 143 1–40.
-
- Chatterjee S and Shao Q-M (2011). Non-normal approximation by Stein’s method of exchangeable pairs with application to the Curie–Weiss model. Ann. App. Probab. 21, 464–483.
-
- Chen L, Goldstein L and Shao Q-M (2010). Normal Approximation by Stein’s Method. Springer Verlag.
Grants and funding
LinkOut - more resources
Full Text Sources
