Direct Feedback Alignment With Sparse Connections for Local Learning

Abstract

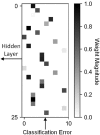
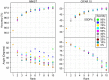
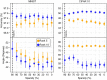
Recent advances in deep neural networks (DNNs) owe their success to training algorithms that use backpropagation and gradient-descent. Backpropagation, while highly effective on von Neumann architectures, becomes inefficient when scaling to large networks. Commonly referred to as the weight transport problem, each neuron's dependence on the weights and errors located deeper in the network require exhaustive data movement which presents a key problem in enhancing the performance and energy-efficiency of machine-learning hardware. In this work, we propose a bio-plausible alternative to backpropagation drawing from advances in feedback alignment algorithms in which the error computation at a single synapse reduces to the product of three scalar values. Using a sparse feedback matrix, we show that a neuron needs only a fraction of the information previously used by the feedback alignment algorithms. Consequently, memory and compute can be partitioned and distributed whichever way produces the most efficient forward pass so long as a single error can be delivered to each neuron. We evaluate our algorithm using standard datasets, including ImageNet, to address the concern of scaling to challenging problems. Our results show orders of magnitude improvement in data movement and 2× improvement in multiply-and-accumulate operations over backpropagation. Like previous work, we observe that any variant of feedback alignment suffers significant losses in classification accuracy on deep convolutional neural networks. By transferring trained convolutional layers and training the fully connected layers using direct feedback alignment, we demonstrate that direct feedback alignment can obtain results competitive with backpropagation. Furthermore, we observe that using an extremely sparse feedback matrix, rather than a dense one, results in a small accuracy drop while yielding hardware advantages. All the code and results are available under https://github.com/bcrafton/ssdfa.

Keywords: backpropagation; bio-plausible algorithms; feedback alignment; hardware acceleration; local learning; sparse neural networks.

Figure 1

Hardware implementations of inference. Comparing von Neumann architecture with distributed memory architecture to avoid bottleneck. (A) Inference constrained by von Neumann architectures. In traditional backpropagation, weight updates not only depend on error but also the other weights. This prevents a distributed architecture. (B) Unconstrained inference. Using Direct Feedback Alignment, inference can be distributed and parallel because weight updates depend only on the error and random feedback values.

Figure 2

A sparse feedback matrix where each hidden neuron is connected to a single error. Only one of the 10 connections between a neuron and error is non-zero.

Figure 3

Neuron-level memory dependence of the different algorithms. (A) Backpropagation: the error at the first layer is computed using all the weights in the deeper layers. This is the weight transport problem. (B) DFA: the error at the first layer is only e · B. This solves weight transport, however it still requires 1,000 FB weights. (C) SSDFA: the error at the first layer is dependent only on a single error and a single feedback weight.

Figure 4

Data movement through the substrate of different algorithms. (A) Backpropagation: in traditional von Neumann architectures weights and activations from the forward pass must be accessed from main memory. The majority of data transfer occurs when moving the large weight matrices from main memory to compute. (B) DFA: in a local learning implementation only the error vector needs to be sent to the neurons. In this case the neuron must receive all N errors and store an additional N random feedback weights. (C) SSDFA: in the single sparse connection implementation of DFA, only a single error needs to be sent to each neuron and only a single random feedback constant needs to be stored. This reduces the bandwidth requirement and feedback weight storage by a factor of N.

Figure 5

Accuracy and angle (in degrees) vs. rank for MNIST and CIFAR10 fully connected networks. Data points are grouped by sparsity, and averaged over 10 different simulations.

Figure 6

Accuracy and angle vs. sparsity. Results from rank 5 and 10 are shown with bars showing the standard deviation for 10 different simulations.

Figure 7

Filters acquired from training AlexNet with BP (A) and DFA (B). Filters for BP show shape and spatial structure, while filters from DFA are random.

Figure 8

Total number of MACs and Data Movement (in MB) for a single training example on CIFAR100 (A,B) and ImageNet (C,D) across BP, DFA, and SDFA.