Dynamic Causal Modelling of Active Vision
- PMID: 31182633
- PMCID: PMC6687902
- DOI: 10.1523/JNEUROSCI.2459-18.2019
Dynamic Causal Modelling of Active Vision
Abstract
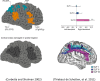
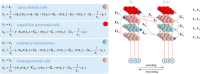
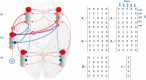
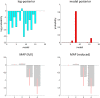
In this paper, we draw from recent theoretical work on active perception, which suggests that the brain makes use of an internal (i.e., generative) model to make inferences about the causes of sensations. This view treats visual sensations as consequent on action (i.e., saccades) and implies that visual percepts must be actively constructed via a sequence of eye movements. Oculomotor control calls on a distributed set of brain sources that includes the dorsal and ventral frontoparietal (attention) networks. We argue that connections from the frontal eye fields to ventral parietal sources represent the mapping from "where", fixation location to information derived from "what" representations in the ventral visual stream. During scene construction, this mapping must be learned, putatively through changes in the effective connectivity of these synapses. Here, we test the hypothesis that the coupling between the dorsal frontal cortex and the right temporoparietal cortex is modulated during saccadic interrogation of a simple visual scene. Using dynamic causal modeling for magnetoencephalography with (male and female) human participants, we assess the evidence for changes in effective connectivity by comparing models that allow for this modulation with models that do not. We find strong evidence for modulation of connections between the two attention networks; namely, a disinhibition of the ventral network by its dorsal counterpart.SIGNIFICANCE STATEMENT This work draws from recent theoretical accounts of active vision and provides empirical evidence for changes in synaptic efficacy consistent with these computational models. In brief, we used magnetoencephalography in combination with eye-tracking to assess the neural correlates of a form of short-term memory during a dot cancellation task. Using dynamic causal modeling to quantify changes in effective connectivity, we found evidence that the coupling between the dorsal and ventral attention networks changed during the saccadic interrogation of a simple visual scene. Intuitively, this is consistent with the idea that these neuronal connections may encode beliefs about "what I would see if I looked there", and that this mapping is optimized as new data are obtained with each fixation.
Keywords: active vision; attention; dynamic causal modelling; eye-tracking; magnetoencephalography; visual neglect.
Copyright © 2019 Parr et al.
Figures


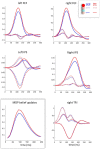
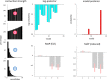
References
-
- Andreopoulos A, Tsotsos J (2013) A computational learning theory of active object recognition under uncertainty. Int J Comput Vis 101:95–142. 10.1007/s11263-012-0551-6 - DOI
-
- Barlow HB. (1961) Possible principles underlying the transformations of sensory messages. In: Sensory communication (Rosenblith W, ed), pp 217–234. Cambridge, MA: MIT.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
