Subjectivity and complexity of facial attractiveness

Abstract

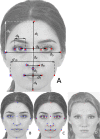
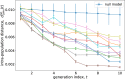
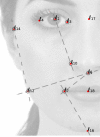
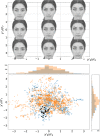
The origin and meaning of facial beauty represent a longstanding puzzle. Despite the profuse literature devoted to facial attractiveness, its very nature, its determinants and the nature of inter-person differences remain controversial issues. Here we tackle such questions proposing a novel experimental approach in which human subjects, instead of rating natural faces, are allowed to efficiently explore the face-space and "sculpt" their favorite variation of a reference facial image. The results reveal that different subjects prefer distinguishable regions of the face-space, highlighting the essential subjectivity of the phenomenon. The different sculpted facial vectors exhibit strong correlations among pairs of facial distances, characterising the underlying universality and complexity of the cognitive processes, and the relative relevance and robustness of the different facial distances.

Figure 1

(A) The parameters defining the face space. The red points indicate the landmarks, α = 1, …, 18, whose 2D varying Cartesian coordinates generate the continuum of face space. The face space points are parametrised in terms of vectors f whose components are the Cartesian coordinates of a set of non-redundant landmarks ${\overrightarrow{\ell }}_{\alpha }$ (signaled with an empty circle), or in terms of (vertical or horizontal) distances d_i (i = 0, …, 10) among some pairs of landmarks $d_i=|x_{\alpha (i)}-x_{\beta (i)}|$ or $d_i=|y_{\alpha (i)}-y_{\beta (i)}|$ (arrows). (B) Reference portrait RP1 used in experiment E1 along with its corresponding landmarks (in blue). (C) Image deformation of RP1 according to a given vector of inter-landmark distances d: the blue reference portrait landmarks are shifted (leading to the red points) so that their inter-landmark distances are d, and the reference image (B) is consequently deformed. (D) Image deformation of the reference portrait RP2 according to the same vector of distances d as in (C).

Figure 2

Intra-population distance of the populations sculpted by different subjects (s) as a function of the generation (t). The Euclidean metrics in face space has been used (see Supplementary Sec. S4), although the results are qualitatively equal for other relevant metrics. Each curve corresponds to a different subject (for 10 randomly chosen subjects). The upper curve of joined circles corresponds to the null model genetic experiment, in which the left/right choices are random.

Figure 3

Main panel: Normalised histograms of pseudo-distances. Blue: subject intra-population distances, or self-distances of all the populations sculpted in E1. Orange: self-consistency distances, or distances among couples of populations sculpted by the same subject in E2. Green: inter-subject distances, or distances among couples of populations sculpted by different subjects in E1. Purple: distances among couples of populations sculpted by different subjects in different experiments, E1 and E3 (differing in the reference portrait). Red: distances among couples of populations sculpted by subjects of different gender in E1. The orange and green arrowed segments over the self-consistency and inter-subject histograms indicate the confidence intervals of the histogram averages, ${\mu }_{\mathrm{sc}}\pm {\sigma }_{\mathrm{sc}}/n_{\mathrm{sc}}^{\mathrm{1/2}}$ and ${\mu }_{\mathrm{i}}\pm {\sigma }_{\mathrm{i}}/n_{\mathrm{i}}^{\mathrm{1/2}}$ respectively, with n_sc = S_scm(m − 1)/2 and n_i = S₁(S₁ − 1)/2.

Figure 4

Relevant inter-landmark segments. The correlation matrix elements C_ij involving vertical and horizontal landmark coordinates, $⟨x_{\alpha (i)}{y}_{\alpha (j)}⟩$ can be understood geometrically as a statistical invariance of the value of some inter-landmark segment slopes (dashed lines) with respect to their average value (represented in the figure). The sign of oblique C_ij’s coincide with that of the slope of the inter-landmark lines $(⟨y_{\alpha (i)}⟩-⟨y_{\alpha (j)}⟩)/(⟨x_{\alpha (i)}⟩-⟨x_{\alpha (j)}⟩)$. For instance, the most correlated horizontal-vertical landmarks are 〈x₁₂y₉〉, exhibiting a positive sign (c.f. Supplementary Table S4): indeed, for lower nose endpoints (which correspond to a positive fluctuation y₉ > 〈y₉〉), the 9–12 angle can be restored only by increasing the x₁₂-coordinate, x₁₂ > 〈x₁₂〉.

Figure 5

Top figure: facial images corresponding to the deformation of the average facial vector along two different principal axes (the e⁽⁷⁾, e⁽⁹⁾ eigenvectors of the correlation matrix C, corresponding to the fourth and second larger eigenvalues, λ₇, λ₉). The axes represent the principal components along these axes, (y′₉, y′₇) in units of their standard deviations (${\lambda }_i^{\mathrm{1/2}}$). In other words, the image is generated from the facial vector $y=E^{†}({y\prime }_7{\mathbf{e}}^{\mathrm{(7)}}+{y\prime }_9{\mathbf{e}}^{\mathrm{(9)}})$. Bottom figure: selected facial vectors. Each point is a projection of a selected facial vector in the principal axes corresponding to the Top figure, i.e., each point has coordinates ${y\prime }_7^{(s,n)},{y\prime }_9^{(s,n)}$, for all s, n in the E1 dataset. Blue points correspond to male subjects, and orange triangles to female subjects (male subjects tend to sculpt vectors with ${y\prime }_9<0$, and vice-versa). The black points correspond to a population sculpted by a single, randomly selected, subject.