Sequence and structural patterns detected in entangled proteins reveal the importance of co-translational folding

Abstract

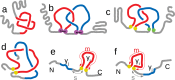
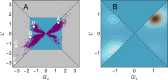
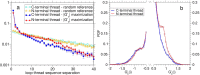
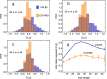
Proteins must fold quickly to acquire their biologically functional three-dimensional native structures. Hence, these are mainly stabilized by local contacts, while intricate topologies such as knots are rare. Here, we reveal the existence of specific patterns adopted by protein sequences and structures to deal with backbone self-entanglement. A large scale analysis of the Protein Data Bank shows that loops significantly intertwined with another chain portion are typically closed by weakly bound amino acids. Why is this energetic frustration maintained? A possible picture is that entangled loops are formed only toward the end of the folding process to avoid kinetic traps. Consistently, these loops are more frequently found to be wrapped around a portion of the chain on their N-terminal side, the one translated earlier at the ribosome. Finally, these motifs are less abundant in natural native states than in simulated protein-like structures, yet they appear in 32% of proteins, which in some cases display an amazingly complex intertwining.

Figure 1

Sketches of proteins with (a) a knot, (b) two linked loops with cysteine closures (magenta dots), (c) two linked loops with virtual non-covalent closures (yellow and green dots form two different contacts), and (d) a loop (red) intertwined with an open chain portion (blue) - a “thread”. (e) A configuration with the loop (γ_i) closer to the C-terminus than the thread (γ_j), and (f) one with the loop closer to the N-terminus. In the two latter pictorial representations of non-structured proteins, we also show the loop-thread sequence separation s and the loop length m.

Figure 2

Some examples of protein domains with nontrivial entanglement, in which one notes a looped portion (red, with yellow ends, following the color code of Fig. 1d) intertwined with another portion of the protein, a thread (blue). (a) protein 2bjuA02, with L′ = 1.145 (also the blue chain contains a loop) and ${G\prime }_c$ = 1.285 of similar magnitude; (b) protein 3thtA01, with significant entanglement (${G\prime }_c$ = −1.56) but without two linked loops (L′ = −0.34); (c) protein 3tnxA00, with large ${G\prime }_c$ = −3.07, while L′ = −1.31 is much smaller and with the same sign; (d) protein 2i06A01, with $L\prime =0.74\simeq 1$, partitioned in the two corresponding linked loops and thus following the color code of Fig. 1c (green ends of the blue loop); (e) again 2i06A01, with ${G\prime }_c$ = −1.26, highlighting the related loop-thread partition. In the last two points one notes that the sign of L′ is opposite to the sign of ${G\prime }_c$. It is an example of the coexistence of different forms of entanglement in the same protein domain. (f) protein 1otjA00, one of the protein domains with largest (absolute) Gaussian Entanglement, with ${G\prime }_c$ = −3.24 and L′ = −3.02. The red loop, with yellow ends, is extremely entangled with the blue portion (which in this case also contains a loop).

Figure 3

(A) Plot of L′ vs ${G\prime }_c$ for each protein in the CATH database; the five proteins shown in Fig. 2a–f are highlighted with the corresponding letter. (B) Smoothed histogram of data with significant linking (|L′| > 1/2). The highest probability is around ${G\prime }_c\simeq L\prime \simeq 1$. The data with the values of L′ and ${G\prime }_c$ computed for each protein in the CATH database are available at http://researchdata.cab.unipd.it/id/eprint/123.

Figure 4

(a) For four cases (see legend), distributions of the loop-thread sequence separation s. Error bars are based on the effectively independent countings determined through the clustering procedure. (b) For the separate cases of N- and C-terminal threads (see legend), tails of the distributions of the loop entanglement for |${G\prime }_c$(i)| > 1/2. Error bars are based on the effectively independent countings determined through the clustering procedure.

Figure 5

For both natural protein domains of length n in the range 55 ≤ n ≤ 64 from the CATH database, and the VAL60 ensemble of homopolypeptides, we plot the normalized histogram of ${G\prime }_c$(i) for loops of length m in the intervals 20 ≤ m ≤ 24 (a), 30 ≤ m ≤ 34 (b), and 40 ≤ m ≤ 44 (c). (d) For natural protein domains and the VAL60 ensemble, root mean squared ${G\prime }_c$(i) as a function of the loop length m.

Figure 6

Scatter plot of the enrichment score ΔE_enr(a, b) vs normal contact potential E_norm(a, b). Each point is for an amino acid pair (a, b) and is colored according to amino acid types: black for pairs of aromatic residues (HIS, PHE, TRP, TYR); magenta for CYS-CYS; green for the rest. The dashed line is a linear fit with slope −0.12. Error bars are computed with a boostrapping procedure and we plot only errors for ΔE_enr as those for E_norm are smaller than the symbol size.

Figure 7

(a) Normal contact potential E_norm; amino acids are ranked from left to right (top to bottom) with increasing average E_norm (over row/column). (b) Enrichment score ΔE_enr for entangled contacts. Different backgrounds are used for highlighting negative and positive values: blue for E < −E₀, light blue for −E₀ ≤ E ≤ 0, pink for 0 < E ≤ E₀, and red for E > E₀ with E₀ = 35. White is used for scores that differ from zero less than the corresponding statistical uncertainty, computed by means of a bootstrapping procedure.