Optimized quantification of spin relaxation times in the hybrid state

Abstract

Purpose: The optimization and analysis of spin ensemble trajectories in the hybrid state-a state in which the direction of the magnetization adiabatically follows the steady state while the magnitude remains in a transient state.

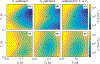
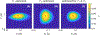
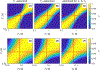
Methods: Numerical optimizations were performed to find spin ensemble trajectories that minimize the Cramér-Rao bound for ${\text{T}}_1$ -encoding, ${\text{T}}_2$ -encoding, and their weighted sum, respectively, followed by a comparison between the Cramér-Rao bounds obtained with our optimized spin-trajectories, Look-Locker sequences, and multi-spin-echo methods. Finally, we experimentally tested our optimized spin trajectories with in vivo scans of the human brain.

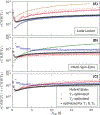
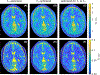
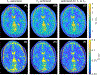
Results: After a nonrecurring inversion segment on the southern half of the Bloch sphere, all optimized spin trajectories pursue repetitive loops on the northern hemisphere in which the beginning of the first and the end of the last loop deviate from the others. The numerical results obtained in this work align well with intuitive insights gleaned directly from the governing equation. Our results suggest that hybrid-state sequences outperform traditional methods. Moreover, hybrid-state sequences that balance ${\text{T}}_1$ - and ${\text{T}}_2$ -encoding still result in near optimal signal-to-noise efficiency for each relaxation time. Thus, the second parameter can be encoded at virtually no extra cost.

Conclusions: We provided new insights into the optimal encoding processes of spin relaxation times in order to guide the design of robust and efficient pulse sequences. We found that joint acquisitions of ${\text{T}}_1$ and ${\text{T}}_2$ in the hybrid state are substantially more efficient than sequential encoding techniques.

Keywords: HSFP; MRF; SSFP; optimal control; parameter mapping; quantitative MRI.

FIGURE 1

Equation (1) describes the spin dynamics and is visualized in (A). The white area indicates the steady-state ellipse which separates the area in which the magnetization grows (red) and shrinks (blue). This particular sub-figure is valid for the ratio T₁∕T₂ = 781 ms∕65 ms ≈ 12, which are values reported for brain white matter. The derivatives of Equation (1) with respect to T₁ and T₂ are depicted in (B) and (C), respectively. These plots are normalized by the respective relaxation times and are, therefore, valid for any combination of T₁ and T₂

FIGURE 2

The spin dynamics in inversion recovery balanced hybrid-state free precession (IR-bHSFP) sequences are depicted on Bloch-spheres (A, D, G, J, M, and P). The polar angle patterns are shown in (B, E, H, K, N, and Q), with the color scale providing a reference for the trajectories on the Bloch-sphere. The absolute value of the magnetization (with a negative sign indicating the southern hemisphere) and its normalized derivatives with respect to the relaxation times are the foundation of the relative Cramér-Rao bound and are shown in (C, F, I, L, O, and R). The optimizations depicted in the left-hand column are limited to 0 ≤ ϑ ≤ π/2, while the right-hand column shows the same optimizations with the limit 0 ≤ ϑ ≤ π/4

FIGURE 3

The depicted relative Cramér-Rao bounds are defined by Equations (4) and (5) and can be understood as a lower bound of the squared inverse SNR efficiency per unit time. They result from numerical optimization for rCRB(T₁), rCRB(T₂), and rCRB(T₁) + rCRB(T₂), while limiting the polar angle to 0 ≤ ϑ ≤ π/2 (lightly colored markers) and 0 ≤ ϑ ≤ π/4 (dark colored markers), respectively

FIGURE 4

The performance of IR-bHSFP sequences optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is illustrated through plots of the relative Cramér-Rao bounds, which provide a lower bound for the noise in the estimated relaxation times. All patterns were optimized for T₁ = 781 ms and T₂ = 65 ms, as indicated by the red square, and were tested for the entire parameter space in a sample MRF dictionary. Note the logarithmic scale in all three dimensions

FIGURE 5

The performance of IR-bHSFP optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is illustrated through plots of the correlation of the fingerprint using the optimization parameters T₁ = 781 ms and T₂ = 65 ms (red square) with the rest of the parameter space

FIGURE 6

The performance of IR-bHSFP optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is depicted through plots of the correlation coefficient. The correlation matrix was calculated for the entire parameter space. Thereafter, a maximum intensity projection was performed along the T₂ (A-D) and the T₁-dimension (E-H), respectively. The result can be understood as the worst case correlations for a single parameter under consideration of all values of the other parameter. The red lines indicates the set of parameters used for optimizing the patterns

FIGURE 7

The in vivo data were acquired with the excitation patterns depicted in Figure 2K, N, and Q with the limit 0 ≤ ϑ ≤ π/4. The parameter maps have an in-plane resolution of 1 mm and were acquired in 3.8 s. Note the logarithmic scale of the T₁ and T₂ color maps

FIGURE 8

The parameter maps are the average of 49 measurements like the one shown in Figure 7, each acquired in 3.8 s with a 10 s pause in between. Note the logarithmic scale of the T₁ and T₂ color maps. The red rectangles indicate the regions of interest used for calculating the values in Table 1

FIGURE 9

In order to verify the theoretically derived noise properties, we depict the mean relaxation times divided by the standard deviation over the 49 consecutive experiments. This metric provides an analog to the signal-to-noise ratio. The upper limit of this metric is directly proportional to the square root of the inverse rCRB(T_1,2)