Invasion reproductive numbers for periodic epidemic models
- PMID: 31193521
- PMCID: PMC6531838
- DOI: 10.1016/j.idm.2019.04.002
Invasion reproductive numbers for periodic epidemic models
Erratum in
-
Erratum regarding missing Declaration of Competing Interest statements in previously published articles.Infect Dis Model. 2020 Dec 17;6:1260. doi: 10.1016/j.idm.2020.12.004. eCollection 2021. Infect Dis Model. 2020. PMID: 34938927 Free PMC article.
Abstract
There are many cases within epidemiology where infections compete to persist within a population. In studying models for such cases, one of the goals is to determine which infections can invade a population and persist when other infections are already resident within the population. Invasion reproductive numbers (IRN), which are tied to the stability of boundary endemic equilibria, can address this question. By reinterpreting resident infections epidemiologically, this study extends methods for finding IRNs to periodic systems, and presents some examples which illustrate the often complex computations required. Results identify conditions under which a simple time-average can be used to derive IRNs, and apply the methods to examine how seasonal fluctuations in influenza incidence facilitate the year-round persistence of bacterial respiratory infections.
Keywords: Basic reproductive number; Mathematical epidemiology; Periodic models.
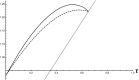
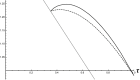
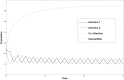
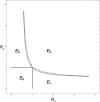
Figures

References
-
- Aulbach B., Wanner T. The Hartman-Grobman Theorem for Carathéodory-type differential equations in Banach spaces. Nonlinear Analysis. 2000;40:91–104.
-
- Bacäer N. Approximation of the basic reproductive number R0 for vector-borne diseases with a periodic vector population. Bulletin of Mathematical Biology. 2007;69:1067–1091. - PubMed
-
- Bacaër N., Ait Dads E.H. On the biological interpretation of a definition for the parameter R0 in periodic population models. Journal of Mathematical Biology. 2012;65:601–621. - PubMed
-
- Bacäer N., Guernaoui S. The epidemic threshold of vector-borne disease with seasonality. Journal of Mathematical Biology. 2006;53:421–436. - PubMed
LinkOut - more resources
Full Text Sources

