Being right matters: Model-compliant events in predictive processing

Abstract

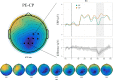
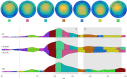
While prediction errors (PE) have been established to drive learning through adaptation of internal models, the role of model-compliant events in predictive processing is less clear. Checkpoints (CP) were recently introduced as points in time where expected sensory input resolved ambiguity regarding the validity of the internal model. Conceivably, these events serve as on-line reference points for model evaluation, particularly in uncertain contexts. Evidence from fMRI has shown functional similarities of CP and PE to be independent of event-related surprise, raising the important question of how these event classes relate to one another. Consequently, the aim of the present study was to characterise the functional relationship of checkpoints and prediction errors in a serial pattern detection task using electroencephalography (EEG). Specifically, we first hypothesised a joint P3b component of both event classes to index recourse to the internal model (compared to non-informative standards, STD). Second, we assumed the mismatch signal of PE to be reflected in an N400 component when compared to CP. Event-related findings supported these hypotheses. We suggest that while model adaptation is instigated by prediction errors, checkpoints are similarly used for model evaluation. Intriguingly, behavioural subgroup analyses showed that the exploitation of potentially informative reference points may depend on initial cue learning: Strict reliance on cue-based predictions may result in less attentive processing of these reference points, thus impeding upregulation of response gain that would prompt flexible model adaptation. Overall, present results highlight the role of checkpoints as model-compliant, informative reference points and stimulate important research questions about their processing as function of learning und uncertainty.

Fig 1

(A) Exemplary trial succession and time frame of the corresponding response for ordered sequences. Sequential trials have been highlighted for illustrative purposes. (B) Schematic structure of a short ordered sequence showing the positions of checkpoints (CP) and prediction errors (PE, red). At the fourth position, the sequence could either be terminated (PE) or continued as expected (CP). Similarly, the sixth position contained either the regular end (CP) or an unexpected extension of the sequence (PE). (C) Cue-based expected sequence length and resulting prediction errors for terminated and extended short ordered sequences (expectation compliance). (D) Local transition probabilities for terminated, regular, and extended sequences depending on the respective level of irreducible uncertainty.

Fig 2

(A) Mean count of false alarms (FA) and misses per block as well as mean PR score as a function of uncertainty. (B) Mean offset latencies for terminated, regular, and extended sequences as well as mean onset latencies for learned and new cue colours during post-measurement. ** = p < .01, *** = p < .001.

Fig 3

(A) Individual gains in reaction time (defined as the difference in reaction time following new minus learned cues) during post-measurement. Positive values indicate quicker button presses following learned cues. Blue dotted line depicts Mdn_Diff = 78.70 ms. Participants were consequently median-split into a gain group (blue) and a no gain group (red). (B) Upper panel: Mean offset latencies as a function of expectation compliance for gain (blue) and no gain group (red). Significant differences only shown for high vs low uncertainty for the sake of clarity (see Fig 2B for differences between levels of expectation compliance). Lower panel: Correlations between offset latency and trial-specific surprise value of sequential extensions for both groups. ** = p < .01.

Fig 4

(A) Mean count of button releases during the experiment up to selected offset latencies for gain (blue) and no gain group (red). Shown here for an exemplary short extended sequence (length of 7 digits), the gain group was found to release the response button more frequently at offset latencies between -1000 and +500 ms (i.e. between the onset of the unexpected sequential digit [red frame] and the offset of the first non-sequential) following extended sequences. Dotted lines and bars depict mean offset latencies for regular sequences per group ± 2 SEM. (B) Similarly, shown here for a short regular sequence (length of 5 digits), the gain group was found to release the response button more frequently at offset latencies between -500 and +500 ms (i.e. between the onset of the last sequential digit and the offset of the first non-sequential digit) following regular sequences. Dotted lines and bars depict mean offset latencies for extended sequences per group ± 2 SEM.

Fig 5

(A) Significant ERP differences between prediction errors and sequential standards included a parieto-central P3b (left) as well as a right-lateralised P600 component peaking over electrode P6 (right). P3b topography shows the frontal and parietal subsets of electrodes used for the analysis (bottom left). Significant clusters are marked in bold. (B) ERP differences between checkpoints and sequential standards were equally reflected in significant P3b (left) and P600 components (right). Respective bottom panels show component evolution over time (all electrodes, no temporal constraints).

Fig 6

Grand averaged ERPs of low (top row) vs high uncertainty checkpoints (bottom row) and sequential standards. Checkpoints elicited significant P3b (left) and P600 components (right) irrespective of the uncertainty level. Note that, while uncertainty did not modulate P3b scalp distribution or peak latency, the P600 elicited by high uncertainty checkpoints showed an earlier peak and a slightly more frontally distributed topography.

Fig 7. The direct comparison of prediction errors and checkpoints revealed a significant N400 component peaking around 418 ms over parieto-central electrodes.

Bottom panel shows component evolution over time.

Fig 8. Global field power (GFP) of group-averaged ERPs for prediction errors, checkpoints under high/low uncertainty, and sequential standard trials time-locked to stimulus onset.

Coloured segments within the area under the curve depict distinct topographic configurations (template maps, TM) as revealed by hierarchical clustering. Upper panel shows scalp distributions of TM depicted in Box A (TM 11, 12, 2) and B (TM 3, 4, 5, 9). Note that the CP LOW curve was flipped for illustrative purposes only and did not differ in polarity.