Indirect Reference Intervals: Harnessing the Power of Stored Laboratory Data

Abstract

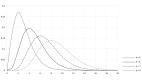
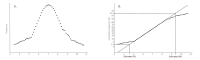
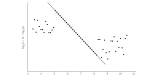
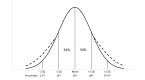
Reference intervals are relied upon by clinicians when interpreting their patients' test results. Therefore, laboratorians directly contribute to patient care when they report accurate reference intervals. The traditional approach to establishing reference intervals is to perform a study on healthy volunteers. However, the practical aspects of the staff time and cost required to perform these studies make this approach difficult for clinical laboratories to routinely use. Indirect methods for deriving reference intervals, which utilise patient results stored in the laboratory's database, provide an alternative approach that is quick and inexpensive to perform. Additionally, because large amounts of patient data can be used, the approach can provide more detailed reference interval information when multiple partitions are required, such as with different age-groups. However, if the indirect approach is to be used to derive accurate reference intervals, several considerations need to be addressed. The laboratorian must assess whether the assay and patient population were stable over the study period, whether data 'clean-up' steps should be used prior to data analysis and, often, how the distribution of values from healthy individuals should be modelled. The assumptions and potential pitfalls of the particular indirect technique chosen for data analysis also need to be considered. A comprehensive understanding of all aspects of the indirect approach to establishing reference intervals allows the laboratorian to harness the power of the data stored in their laboratory database and ensure the reference intervals they report are accurate.

Figure 1

Standard gamma distributions. The shape and scale of the gamma distributions may be ‘parameterised’ in several ways. Here α – shape parameter and β – scale parameter. The standard gamma distributions are those where β = 1.

Figure 2

Graphical representations of a cumulative Gaussian distribution. The cumulative percentage of observations (y-axis) of a dataset is graphed as a function of the value (x-axis). (A) Cumulative frequency plot: Data from a Gaussian distribution is plotted with both axes having a standard linear scale. The resulting graph is sigmoidal-shaped. (B) Normal probability plot: The y-axis has a non-linear scale designed so that the cumulative frequency of Gaussian data appears as a straight line.

Figure 3

Illustration of Hoffmann’s method. A hypothetical mixed dataset is plotted in two ways. (A) Frequency plot: The dataset is seen to follow a Gaussian distribution with distortion in the tails. (B) Normal probability plot: In Hoffmann’s method a line of best fit of the central Gaussian component is drawn. The lower reference limit (LRL) and the upper reference limit (URL) are estimated from the x-values corresponding to y = 2.5% and y = 97.5%, respectively, along this line of best fit. This is the basis of Hoffmann’s original method.

Figure 4

Bhattagram of dataset 3(A). The dataset shown in Figure 3(A) is graphed on a Bhattacharya plot, or ‘Bhattagram’. Log_e(x + h) - log_e(x) is plotted on the y-axis, where h is the data bin width, against the midpoint of the bin on the x-axis. The central Gaussian component of the dataset is visualised as linearly-related points with a negative slope. The mean and standard deviation of the Gaussian component of the dataset can be calculated from the slope and y-intercept of the line of best fit of these data points.

Figure 5

Principles of Pryce’s method: abnormal values on both ends of the distribution. When values from subjects with disease occur on both ends of the distribution Pryce assumes the values from subjects with disease do not significantly affect the mean value from healthy subjects. The standard deviation (SD) is estimated by assessing 34% of the population on either side of the mean. The solid lines represent the Gaussian distribution of values from healthy individuals. The dashed lines represent the distortion of this distribution by values from subjects with disease.

Figure 6

Principles of Pryce’s method: abnormal values on one end of the distribution. When values from subjects with disease occur only on one end of the distribution, Pryce uses the mode (highest frequency value) to estimate the mean of values from healthy subjects. The standard deviation (SD) is estimated by assessing 34% of the population on the side of the mode away from the side of the distribution with abnormal values. The solid lines represent the Gaussian distribution of values from healthy individuals. The dashed lines represent the distortion of this distribution by values from subjects with disease.