Review of Causal Discovery Methods Based on Graphical Models
- PMID: 31214249
- PMCID: PMC6558187
- DOI: 10.3389/fgene.2019.00524
Review of Causal Discovery Methods Based on Graphical Models
Abstract
A fundamental task in various disciplines of science, including biology, is to find underlying causal relations and make use of them. Causal relations can be seen if interventions are properly applied; however, in many cases they are difficult or even impossible to conduct. It is then necessary to discover causal relations by analyzing statistical properties of purely observational data, which is known as causal discovery or causal structure search. This paper aims to give a introduction to and a brief review of the computational methods for causal discovery that were developed in the past three decades, including constraint-based and score-based methods and those based on functional causal models, supplemented by some illustrations and applications.
Keywords: causal discovery; conditional independence; directed graphical causal models; non-Gaussian distribution; non-linear models; statistical independence; structural equation models.
Figures
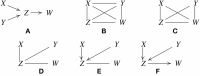
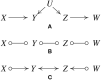
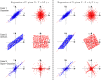
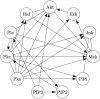
References
-
- Ayesha A. R., Richardson T. S., Spirtes P. (2009). Markov equivalence for ancestral graphs. Ann. Stat. 37, 2808–2837. 10.1214/08-AOS626 - DOI
-
- Butte A. J., Kohane I. S. (2001). Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements, in Pacific Symposium on Biocomputing, 418–429 - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

